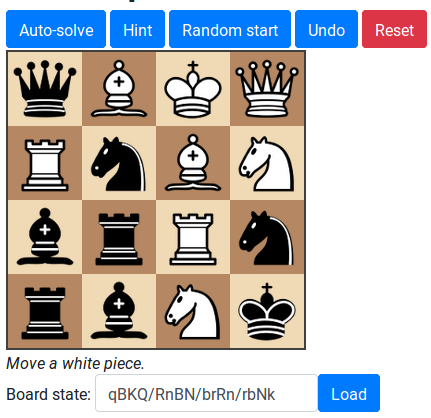
A 4x4 chess puzzle
Tue 28 August 2018Tagged: chess, puzzle
Playing Isopath a lot recently led to a broader interest in board games, which led to me playing a lot of go, and particularly chess (you can add me on lichess, but I'm not very good). I had a look at some single-player variants of chess and played "Hippodrome" a few times but found it very easy, however it gave me an idea for another possibility.
The puzzle
The idea is that a 4x4 board is randomly filled with the 16 pieces from an ordinary chess set, with pawns excluded. You then alternate moving a white piece and then a black piece. Pieces move like in chess, but every turn must be a capture. The game ends either when there is no legal move, or when the white king captures the final black piece on the 15th turn. (I'm aware this isn't the kind of thing people normally expect of a "chess puzzle", but I didn't know what else to call it).
I wrote a web-based implementation of this puzzle using a hacked-up version of chessboardjs to render the 4x4 board and pieces.
Code on github.
Solving it
I think there are around 41 billion unique starting positions. There are 16! = 2.1×1013 possible permutations of 16 unique pieces, but since knights, rooks, and bishops all occur twice per colour, we can divide by 26, leaving 3.3×1011. If we also factor out rotations and mirrors, we can further divide by 8, leaving 4.1×1010, or about 41 billion.
It would be good to come up with a methodical way of solving these puzzles.
If you just play random legal moves, you'll usually find that the puzzle ends up in an unsolvable state with 3 or 4 pieces left. I've come across a few principles that help, but still don't have a general method of solving.
1. When you move a piece, no other piece will ever be able to occupy the square you moved it from
Since every move must capture a piece, no piece can ever move on to an empty square, which means once you've vacated a square, you can never occupy it again.
2. The final move must be a capture by the white king
This follows because every move is a capture, and the game ends when only the white king remains.
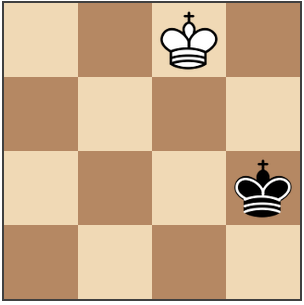
This position is unsolvable: 2K1/4/3k/4 (copy and paste into the "Board state" box to load it in the interface).
3. If the white king is ever left with no pieces adjacent to it, the position is unsolvable
This follows from points 1 and 2. Since the king can only capture pieces adjacent to it, and we know a piece can never occupy a square that is empty, if the white king is surrounded only by empty squares, it is not possible for the white king to ever capture the final black piece that would end the game.
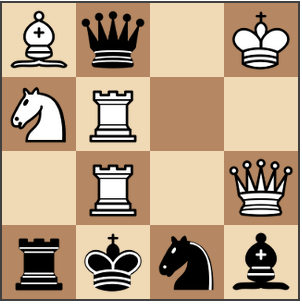
This position is unsolvable: Bq1K/NR2/1R1Q/rknb
4. The penultimate move must be a capture by a black piece of a white piece that is adjacent to the white king
This follows from point 2. Since we know the final move is by white, we know the penultimate move is by black. Since the final move begins with a black piece adjacent to the white king, and there's only one black piece on the board, the previous black move must have moved that piece. Since all moves must be captures, the previous black move must have been that piece capturing a white piece. Since the king can only capture adjacent, the previous black move must have been that piece capturing a white piece that was adjacent to the white king in order for the position to be solvable.
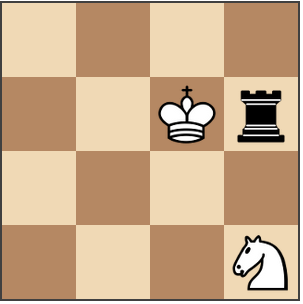
This position is unsolvable: 4/2Kr/4/3N
Black is forced to capture the knight, leaving the king isolated.
5. The move before the penultimate move must leave the white king adjacent to a white piece that can be captured by the only remaining black piece
This follows from point 4. We know the penultimate move must capture a white piece adjacent to the white king, so we know the move before that must leave the position in a state where this is possible.
This can be achieved either by moving the king or the other white piece (at the point this move is played, there are only 2 white pieces). It is possible to draw similar conclusions all the way back to the beginning of the game, but the number of possible moves increases exponentially (maybe?) as you go further back.
This position is unsolvable: 4/2qn/1K2/2N1
Although either of the black pieces can be captured by white, neither move would leave the king adjacent to the other white piece. That means after black has captured the other white piece next turn, the white king will be left isolated.
6. If we can find an efficient way to decide whether a position is solvable, that is easy to turn into a quick solving algorithm
Let's assume we have an oracle that can tell us whether a position is solvable. To decide what move to play, we simply consider every legal move and ask the oracle whether the resulting state is solvable. If it is, we play that move and then repeat.
This sounds superficially similar to a depth-first search, except it only ever has 1 level of backtracking so completes in linear time. It is therefore suitable for carrying out by hand if the oracle is simple enough.
A first approximation is just to consider points 1 to 5 above, and make sure not to play any turn that would leave the board in an obviously-unsolvable state. I'm interested in hearing more simple rules that can disprove solvability of a position.
Empirical analysis
I wrote a go program to solve positions more efficiently than the Javascript version included in the user interface. The general algorithm is the same (depth-first search over all legal moves until a solution is found), but it uses 16-bit bitboards to represent the occupied squares, and lookup tables to calculate legal moves. It's a bit hacky and not user-friendly but should serve as a good base if you want to do some similar analysis.
Of several million random starting positions I tested, every single one was solvable.
I then wondered how many turns you could play at random without creating an unsolvable position. There's no point wasting time reasoning about the first few turns if any legal move would work just as well. I made the program ignore backtracking for the first N turns (i.e. play at "random" for N turns, and only then start backtracking).
I ran the program on 1 million random starting positions for each value of N, with the following results.
| Turns played at random, N | Pieces remaining on board after N turns | Probability of having a solvable position after N random turns |
|---|---|---|
| 0 | 16 | 100% |
| 1 | 15 | 100% |
| 2 | 14 | >99.999% |
| 3 | 13 | 99.6% |
| 4 | 12 | 98.6% |
| 5 | 11 | 93.2% |
| 6 | 10 | 83.9% |
| 7 | 9 | 65.1% |
| 8 | 8 | 49.0% |
| 9 | 7 | 29.7% |
| 10 | 6 | 20.0% |
| 11 | 5 | 9.80% |
| 12 | 4 | 7.70% |
| 13 | 3 | 4.85% |
| 14 | 2 | 4.85% |
| 15 | 1 | 4.85% |
From the 1 million positions tested, all of them were solvable after a random first turn. Only 3 of the 1 million positions were unsolvable after a random second turn.
One of the 3 positions was Nbrn/kqQB/nNRR/rbBK:
If you happen to take the black bishop with the white queen, and then take the white queen with the black rook, you end up with Nr1n/kq1B/nNRR/rbBK:
which has no solution.
For practical purposes, you can play the first 5 turns at random and still usually have a solvable position (93%). With each turn played, reasoning about the position becomes easier. Although it is still too hard for me, in the general case, with 11 pieces still on the board.
Further work
It would be nice if the user interface accepted a "difficulty" setting. We could come up with some algorithm for scoring how difficult a position is (probably based on how sensitive it is to the choice of moves made early on), and then generate starting positions at random until we find one of approximately the desired difficulty.
More progress towards a methodical solving system would also be useful.
Testing against 1 million positions gives a good idea of the numbers for solvability, but the go program is fast enough that it could probably solve all 41 billion unique starting positions in only a day or so if anybody cared to make it do that (you can factor out rotations by enforcing that the white king starts in the top-left quadrant; factoring out mirroring is maybe trickier but would only get another factor of 2 so maybe you can ignore it). I'd be fascinated to see if there are a tiny number of unsolvable starting positions.
The links again: you can play it at https://incoherency.co.uk/chess-puzzle/ and view the code at https://github.com/jes/chess-puzzle.
Let me know if you have anything to say or ask about the chess puzzle, I'd love to hear from you.
If you like my blog, please consider subscribing to the RSS feed or the mailing list: