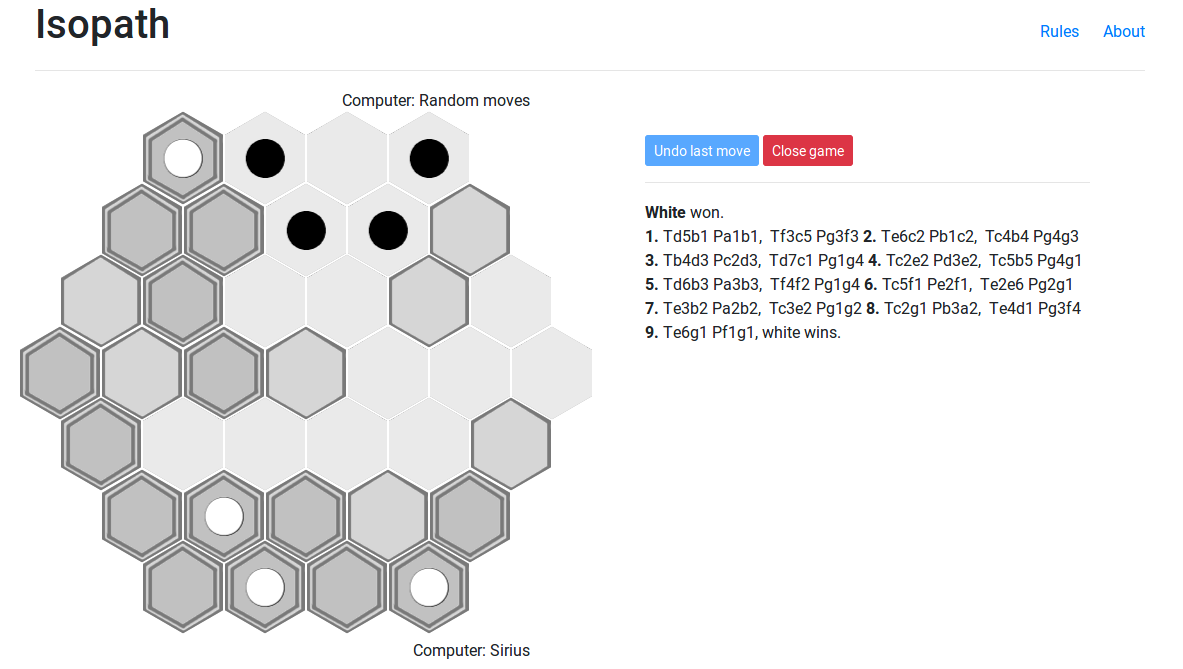
Isopath is a game invented by YouTube user pocket83. The game was initially presented in this video where pocket83 shows how he made the board and tiles, and then explains the game rules from 15:45 onwards. Isopath is a zero-sum, turn-based, deterministc, perfect-information game, which puts it in the same class as games like chess, draughts, go, noughts-and-crosses, etc.
I 3d printed a few sets for myself and some friends, and we've enjoyed playing it. If you like this sort of game, you should try a few rounds of Isopath. I think you'll like it too.
Over the last week I've been working on a browser-based implementation of Isopath, which you can play at https://isopath.jes.xxx/. You can play with a friend either locally or over a websocket connection, or you can play against an AI locally. There are 2 AIs available at the moment, one just plays random moves, and the other is a relatively-serious effort, but not good enough to beat a human who knows its weaknesses.
Rules
The gist is that two players each have 4 pieces on a hexagonal game board, starting at the edges on opposite sides.
One player can only move on top of stacks of 2 tiles, and the other player can only move on the bottom. In each turn a player moves one of their pieces to an adjacent location that is at the correct height, and moves any free tile to any other location on the board. The game ends when one player places a piece in the opponent's home row.
That's not quite all, you can learn the full rules either from pocket83's video, from his rule sheets (sheet 1, sheet 2, sheet 3) , or from my write-up of the rules. You'll get a better feel for the rules by playing the game.
Notation
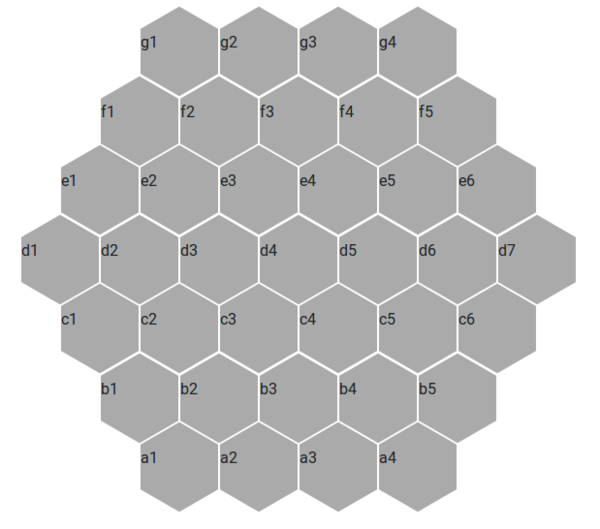
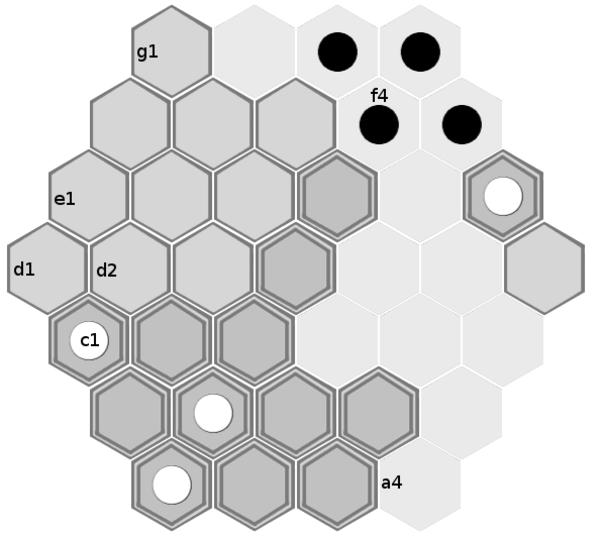
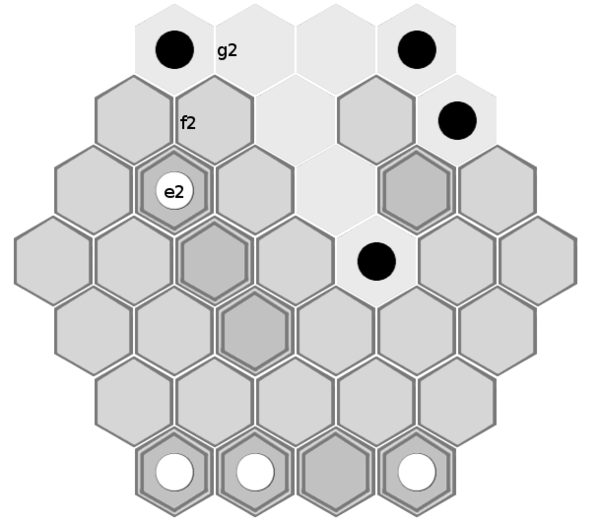
It's helpful to be able to unambiguously identify the spaces on the board. For this reason, I propose labelling the tiles as in this image:
(i.e. the rows are labelled a to g, and the cells within each row are labelled starting with 1 at the left, from white's view).
White always starts on the 'a' row.
For correspondence play (and otherwise), in order to write down the sequence of moves made in the game, we need a move notation. Pocket83 didn't suggest any notation to use, so I am using a capital letter to signify the move part type ('T' for tile, 'P' for piece, 'C' for capture) and then either 1 or 2 coordinates to signify the affected tiles.
For example, moving a tile from a1 to b5 would be "Ta1b5", and capturing a piece at d3 would be "Cd3".
For the sake of consistency, I also propose standardising that white always moves first (this does not affect the nature of the game as everything is symmetrical). A representative game might look like:
1. Td7b3 Pa2b3, Tf3d6 Pg2f3 2. Tc6c4 Pb3c4, Te3e4 Pf3e3 3. Td1d4 Pc4d4, Tf4d5 Pg3f3 4. Te5e2 Pa3b3, Td3d2 Pe3d3 5. Tc1c3 Pb3c3, Tc2d1 Pd3c2 6. Te1b1 Pa1b1, Pc2c1 Ta2c6 7. Tc6b5 Pa4b5, Pf3e3 Ta3e1 8. Tb4c5 Pb5c5, Pg4f4 Td6e6 9. Tb2c2 Pc5c4, Pf4e5 Td6e1 10. Tf2f4 Pc4d5, Pg1g4 Tf4d7 11. Tf5c2 Pc3c2, Td1d3 Pc1d1 12. Tc4d3 Pc2d3, Tb5c4 Pe5d6 13. Ce3 Tf1b4, Tb5b4 Pd6c6 14. Td2g3 Pd4e4, Ta4b2 Pc6b5 15. Te6c1 Pe4d4, Ta4b2 Pb5a4, black wins.
Tactics
Now we get to the meat of what I wanted to talk about.
(Some of the examples are rather contrived and exaggerated, in order to best demonstrate the principles, but never mind that; the principles still apply in normal gameplay).
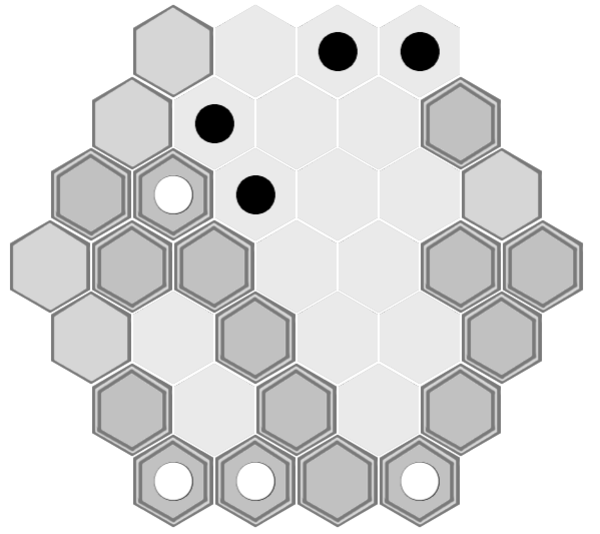
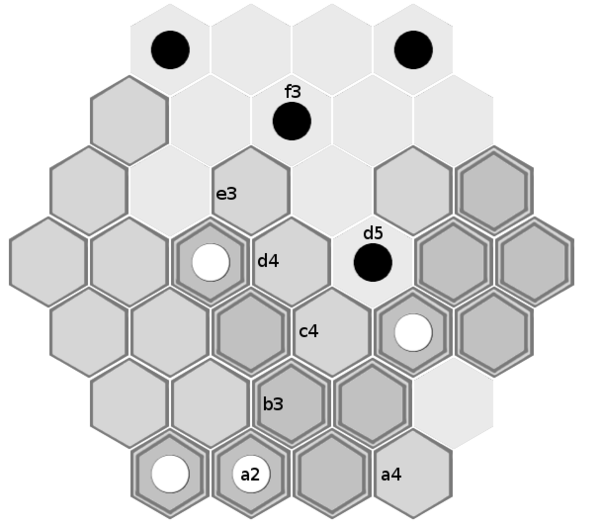
1. A piece can not be stopped from advancing at 1 tile per turn, on a path that has all of the tiles at the correct height, except by threat of capture
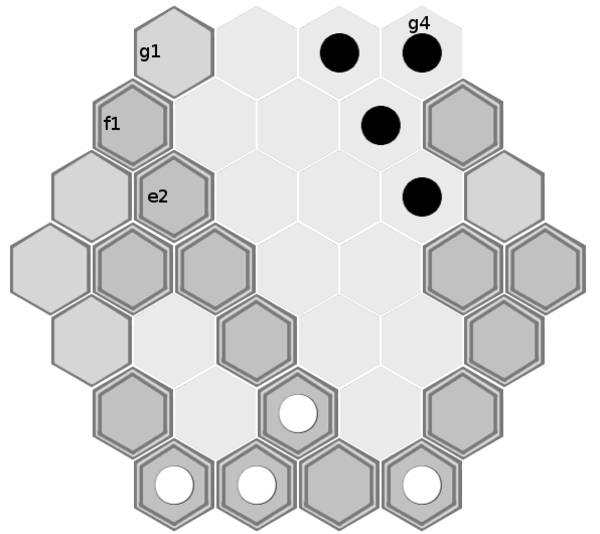
With black to play here, there is nothing black can do to prevent white from winning. Black can remove a tile from white's path each turn, but white can immediately put it back and progress 1 further tile.
Although the spaces g1 and g4 are considered adjacent, black can't teleport from g4 to g1 because white has already placed a tile on g1 (which black is not allowed to remove because it's on his home row).
Black's only chance would be to move 2 of his pieces to threaten capture somewhere along the path. Threatening capture of g1 is no use, because by the time white is on g1 he's already won the game. He can't threaten capture of f1 because he can only get 1 piece adjacent to it. Threatening capture of e2 would work, but it will take black 4 turns to get 2 pieces adjacent to e2, by which point white will already be on e2 and will be able to move off e2 before getting captured. Threatening capture of d3 and c3 will also take 4 turns, but white will get past them even earlier.
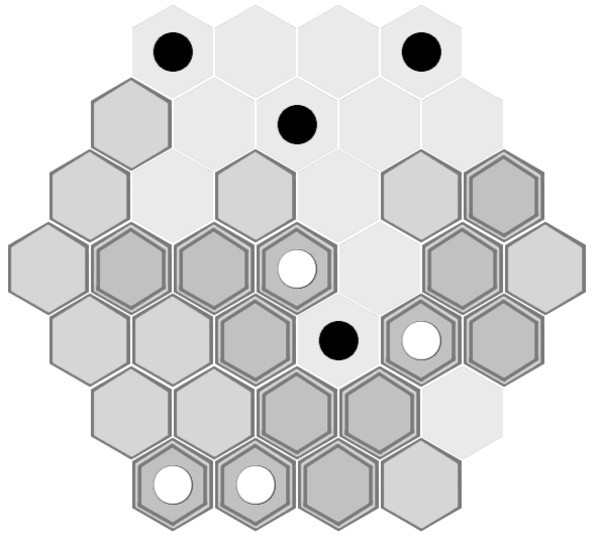
If black does attempt to threaten e2, we reach something like this position, with white to play:
White simply restores the tile on f1, steps on to f1, and then wins in the following turn.
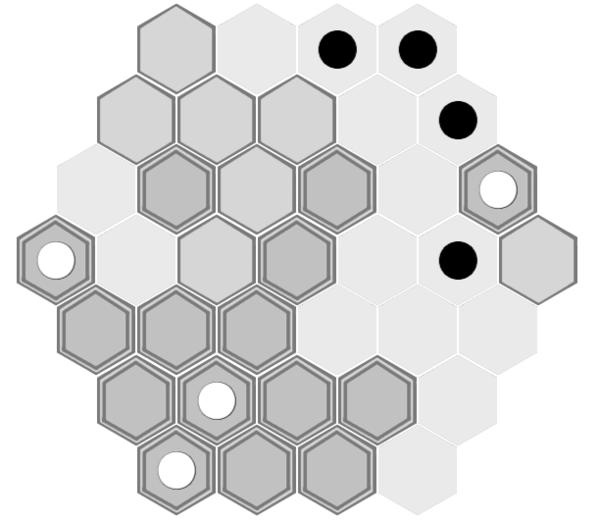
2. A piece can advance at 1 tile per turn, on a path that has all of the tiles at the middle height, except where explicitly stopped
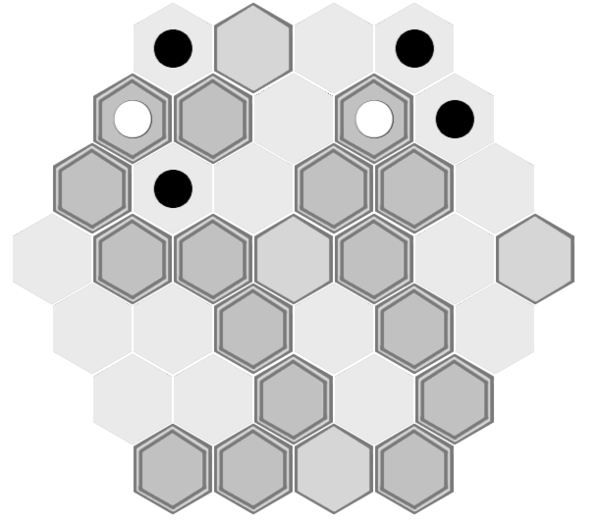
With black to move.
Black was paying attention last time, and knows that his 5-turn path from f4 to a4 can't be stopped by white. However, white's path from c1 to g1, while not at white's full tile height, is potentially 1 turn shorter than black's path if black plays poorly. If black single-mindedly moves his piece towards a4 without concern for which tiles he moves on the board, he'll find that white is able to continue placing 1 tile and moving his piece 1 space per turn, and white will reach g1, winning the game for white, immediately before black is able to step on to a4.
Black should remove the tile from d2 in his first turn, forcing white to move his piece to d1 if he wants to make progress. Black should then remove the tile from e1, leaving white unable to make progress:
Black's best path is now shorter than white's, and black wins the game. (Black could have captured white's piece on e6 on either his second or third turn, but doing so conveys no advantage here. It would mean forgoing either one tile movement or one piece movement, but black would still be able to block white's progress and would still win the game).
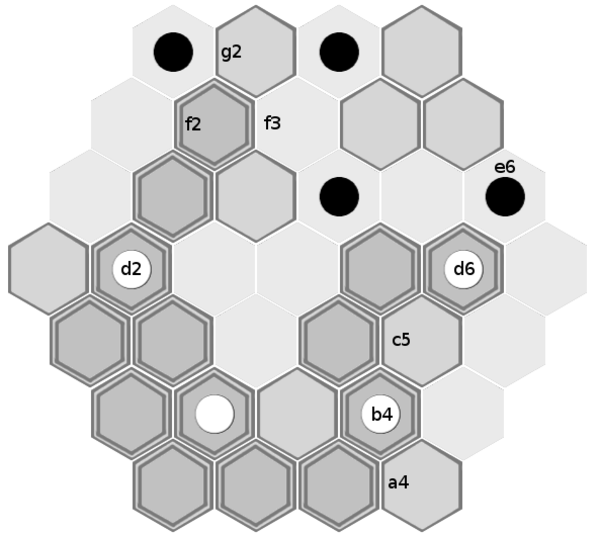
3. It's easier to threaten capture in the middle of the board than at the edges
Black to move.
Black has a path from e6 to a4 that is at his height, so he can't be stopped except by threat of capture. White also has a path from d2 to g2 that is at his height, and white's path is one turn shorter. Unfortunately, white's defensive formation is much weaker than black's, because it does not adequately protect the edges of the board.
The only way white can threaten capture of black's piece as it heads towards a4 is if white can move one of the pieces from b4 or d6 to c5. Therefore black's move is to remove the tile from c5 and start moving towards a4:
- If white responds by trying to block black's progress towards a4, black can just remove the tile and proceed.
- If white responds by trying to restore the tile on c5, black can again remove the tile and proceed.
- If white ignores black's progress and tries to head along his (shorter) path from d2 to g2, black can move a piece on to f3, threatening f2, and then continue heading towards white's home row and win the game.
4. The row immediately in front of your home row is very vulnerable
Once your opponent has a piece on the row immediately in front of your home row, your only way to stop him from winning the game is to threaten him with capture (or to physically have a piece in the way). If you can't, or don't, put him under threat this turn, then he will win. On his next turn he alters a space on your home row by 1 tile, and you can't capture him because you didn't put him under threat last turn. On his turn after that he finishes altering your home row and wins:
White to move. By this point it's too late for black to stop white from winning. White moves a tile on to f2 and moves the piece from e2 to f2. He's now on the row immediately in front of black's home row, so black's only way to stop him is to threaten him with capture. Black can't do that this turn because his pieces are too far away, but he can take 1 step towards. On white's turn he places the first tile on g2 and moves a random piece other than the one on f2. Black can now get close enough to put f2 under threat, but on white's turn he places the second tile on g2 and wins.
Black should have noticed this coming sooner and made sure either not to have his pieces so far away, or to defend the vulnerable row to stop white from being able to step on to it.
(As an aside, I think 2 players who persistently defend this row will end up in a stalemate that neither player can break without losing the game. I'm not sure how the rules could best be tweaked to avoid this, or if doing so is even beneficial).
5. There's no need to fully develop any space on your opponent's home row until the final move that wins you the game
As soon as you have altered a space on your opponent's home row by 1 tile, and because players aren't allowed to touch the tiles on their own home rows: a.) your opponent can no longer stand on that space, for the rest of the game, and b.) your opponent can not undo your building work.
Since every turn consists of 2 parts, you will always be able to perform the final tile move to fully develop your winning space during your final winning move. Therefore, to fully develop any space on your opponent's home row, before the move that wins the game for you, is to rob yourself of one tile move earlier in the game.
(Of course, if any other possible tile move would weaken your position, it's perfectly reasonable to use your opponent's home row instead. But that's rarely, if ever, the case).
6. Forcing a capture by threatening escape routes
If you threaten an opponent with capture, and you also manage to threaten his only escape route, then you can force a capture of his piece.
Here's a position that came up in a game between the AI (white) and me (black), with black to move:
I moved the piece from d5 to c4, to step along the shortest path to a4, expecting white to respond by moving the piece from a2 to b3. I hadn't noticed the "pincer movement" available to white. He moves the piece on to d4, threatening both the black piece and the black piece's escape route:
And from there black has no way to save the piece on c4, because the only immediate escape is threatened, and any other escape route will take at least 2 turns to move on to.
If black had brought forward the piece from f3 sooner, threatening d4, that would have prevented white from being able to move on to d4, making it safer for black to move on to c4. White could still move on to c3 to threaten c4, but black would at least be able to avoid the forced capture.
Puzzle
White to move and win in two:
(To be clear: black's home row is at the top).
More
That's all for now. I hope you enjoyed it. I have developed quite the obsession with Isopath recently, and I think you will too if you give it a try.
In the future I intend to write some more about tactics, and also about the challenges in writing an AI, and promising approaches.
Please get in touch if you want to talk about Isopath, play Isopath, or write an AI to play Isopath: james@incoherency.co.uk.