2025-04-26

Last modified: 2025-04-28 15:09:29

• Isoform
• Blends

Isoform

Progress has stalled because I've been busy with house stuff.

But I think maybe it's time to stop messing about with trying to explore the "breadth" of what is possible with SDF-based CAD, and instead explore the full "depth" of what is required for a Part Design-like workflow.

So that would be:

• make blends more predictable and more reliable
• gears, helical extrusions
• some sort of "timeline" style document view (but still integrate with CSG, Modifiers, etc.)
• sketch attachment
• arcs
• constraints
• parameterisation

And potentially we would want to work out whether constructing a box out of intersections of half-spaces can be done properly.

Blends

On blends I think I need a more rigorous theoretical grounding of what I'm actually trying to achieve.

First attempt:

Do a minimal(-ish) rewrite of the tree, by repeatedly applying the distributivity rule, such that every pair of surfaces that need to be blended are sibling nodes at some point in the tree. And then at every combinator of leaf nodes, set the required blend parameters.

So the issue there is that I don't know if that is actually sufficient to ensure all the blends get applied. Because although the blend between A and B will be applied at Combinator(A, B), if there are more surfaces in the tree, then A and B could get duplicated (by the distributivity rule) and appear in lots of other places, where the blend won't get applied.

So then the question is: is there a way to ensure we apply all blends anyway? Or else: how can we tell which blends can be satisfied and which ones can't?

Or: is tree rewriting even the way to go? Are ideas more like "vary the blend parameters according to the child surfaces" actually superior?

Or: do we actually not want arbitrary targeted blends as such? We want a timeline-like view, and at each step you are allowed to set parameters for blending each of your new surfaces with the entire existing model. And then we just set the blend parameter for the union/intersection that adds each new surface, and no need to rewrite the tree?

I think that last idea might be a good one - if I can convince myself that it allows you to do all useful types of blend.

When you want a blend between 2 surfaces, you have to add it at the step where you've just added the second surface. If that surface intersects more than one existing surface then you'll get blends against all of those surfaces rather than just the one you wanted.

In what circumstances would that be a problem?

Also, with timeline blending, if you add a new feature that has 2 surfaces A and B, and you want surface A to have one blend and surface B to have a different blend... isn't there some risk that you end up adding a blend between A and B? Do we still have to do tree rewriting with distributivity? So does this actually solve anything at all?

What it solves is that at each step we treat the entire pre-existing tree as a single node in the tree that we need to rewrite, and then we are only doing distributivity over a handful of nodes.

I got o3 to see if there are any obvious cases that this will break for. The best one it found was if you make a hole all the way through the existing part and want to chamfer the top but not the bottom.

I wonder if it would help if instead of having to deal with both Union and Intersection, we instead dealt only with min or max, on the basis that min(a,b) = -max(-a,-b)?

o3 has come up with an idea it calls "masked clones". So basically we make an SDF that is a "tube" along the intersection of the 2 surfaces. And inside this "tube" it gives you the blend of the 2 surfaces. And you add the "blend tube" as another child of the LCA of the 2 surfaces. But for example with Unions it only works for adding blends to internal corners, not external ones, because adding an extra child to a Union can only make the shape grow, not shrink.

But I could add a "Tube" combinator and play with it to see what it can do.

Actually it looks like this might do the right thing? Maybe a Union actually does always create an internal corner. Could this actually work?

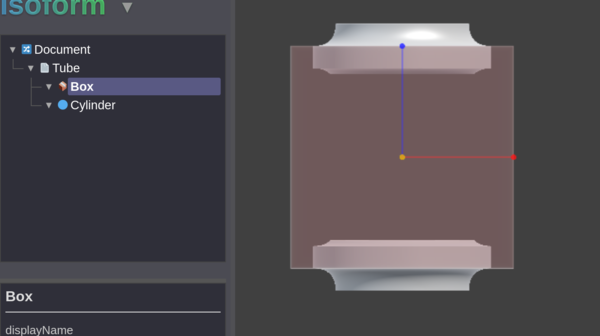
This is a "Tube" of a Box and Cylinder:

So "Tube" is obviously the wrong name, it is just an object that only exists at points in space that are within blendRadius of both surfaces. All of the "Tube" lies "inside" the two objects, except the blend, which is external. So when we Union the Tube with the two objects, we get the blend we desire! So if we add the Tube as a 3rd child of the Union that is the LCA of these 2 nodes, then we get our blend!

Ah, but we also get a "phantom blend" in the parts of space that have already been cut off by other parts of the subtree. Imagine that I wanted a blend between the Box and the Cylinder, but the Cylinder was also cut in half by a half-space. So if we have Union(Box,Intersection(Cylinder,HalfSpace)) and we want a blend between Box and Cylinder, we'd get the "Tube" showing a blend with the entire Cylinder instead of only with the parts of the Cylinder that still exist.

It's saying we can "kill phantoms" by masking again with the actual children of the node we're going to add this as a sibling of. So compute the SDF for the tube, and then Intersect that with the 2 existing child nodes. I don't think that works because then the filleted region disappears as well. Everything outside the 2 child nodes disappears.

Oh, but if we just subtract the radius again on the second go?

So for a blend with radius r between surfaces i and j:

• find the LCA node N of i and j, let's say that's a Union(A,B) where A is a subtree containing i and B is a subtree containing j
• let F(n) be the SDF for a node n
• let dIJ = max(abs(F(i)), abs(F(j)))
• let Fi = max(F(i), dIJ-r)
• let Fj = max(F(j), dIJ-r)
• let Ftube = smoothmin(Fi, Fj, r)
• let Ftube2 = max(Ftube, max(A,B)+r)
• and finally add Ftube2 as a 3rd child of the Union (equivalently, replace N=Union(A,B) in the tree with Union(Ftube2, N))

Maybe something like that? And how does that generalise to intersections?

o3 says:

def add_fillet(N, leaf_i, leaf_j, r, eps=1e-4):
    A, B = pick_child_branches(N, leaf_i, leaf_j)   # immediate children of N
    d    = max(abs(F(leaf_i)), abs(F(leaf_j)))
    Fi   = max(F(leaf_i), d - r - eps)
    Fj   = max(F(leaf_j), d - r - eps)
    Ft   = smoothmin(Fi, Fj, r)
    Mask = min(0, max(A, B))

    if is_union(N):                     # concave
        Fblend = max(Ft, Mask)
        return min(A, B, Fblend)
    else:                               # convex (intersection node)
        Fcut   = -min(Ft, Mask)
        return max(A, B, Fcut)

I haven't tested it yet.