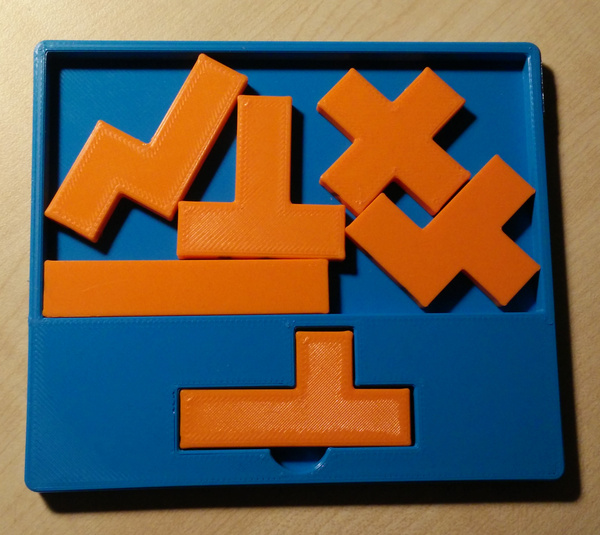Packing puzzle: Six Fit

I've designed a new 2d packing puzzle. It's called "Six Fit" and you have to fit 6 pentominoes into a rectangular tray.

If you want to 3d print it, you can download it from prusaprinters.

I don't know if you're familiar with Stewart Coffin's puzzle "Four Fit" (aka "Martin's Menace" because Martin Gardner said "It looks easy but is fiendishly difficult. I wasted a week trying vainly to solve it"). There is a 3d-printable version of Four Fit on thingiverse.

Four Fit is so difficult because the solution involves placing the pieces so that they are not aligned with the apparent axes of the box you need to put them in.

There is also a "Five Fit" puzzle, available for example here.

However I have not yet been able to find an example of a Six Fit puzzle, so I wrote some code to find one for myself, and I found this one.

Searching for puzzles

My "packominoes" tool generates grids skewed away from the axes. It searches for possible skewings where a section of the skewed grid intersected with an axis-aligned bounding box leaves a given number of squares available. Having found a suitable skewed grid, another program brute forces the set of all sets of pentominoes to try to find a set of pieces which can pack into the skewed grid, but which cannot pack into the largest axis-aligned grid that fits within the axis-aligned bounding box.

A generated puzzle, then, is an axis-aligned bounding box and a set of pieces.

Here's a diagram showing how the skewed grid and the bounding box interact for Six Fit:

There's a bit more info in my packominoes github repository.

More puzzles

I expect it would also be possible to find a Seven Fit and possibly Eight Fit, although the chances get slimmer as the numbers get higher because the number of possible ways to fit the pieces together start making it impossible to find a box that permits a "diagonal" solution without also permitting an "orthogonal" solution. Hope that makes sense.

We could also search for new variations for low-numbered packing puzzles of this type, using different sets of pieces.