Prime Combination: Solution

One solution to the Prime Combination puzzle is 00001 -> 00002 -> 00003 -> 00013 -> 09013 -> 99013 -> 99023 -> 99923 -> 99823 -> 99833 -> 09833 -> 09733 -> 00733 -> 10733 -> 10723.

Mandatory move to 00003

There is a relatively straightforward argument that the first moves must be 00001 -> 00002 -> 00003. Consider:

1. To turn the last digit into a 3 it has to come from either 2 or 4.
2. The only prime ending in 2 or 4 is 00002.
3. Therefore the only way to get a 3 in the final position is 00002 -> 00003.

This cuts down the space of prime numbers we need to search quite considerably, because we only need to consider the ones that end in a 3 (which is only 2402 of the 9592 primes that fit in 5 digits).

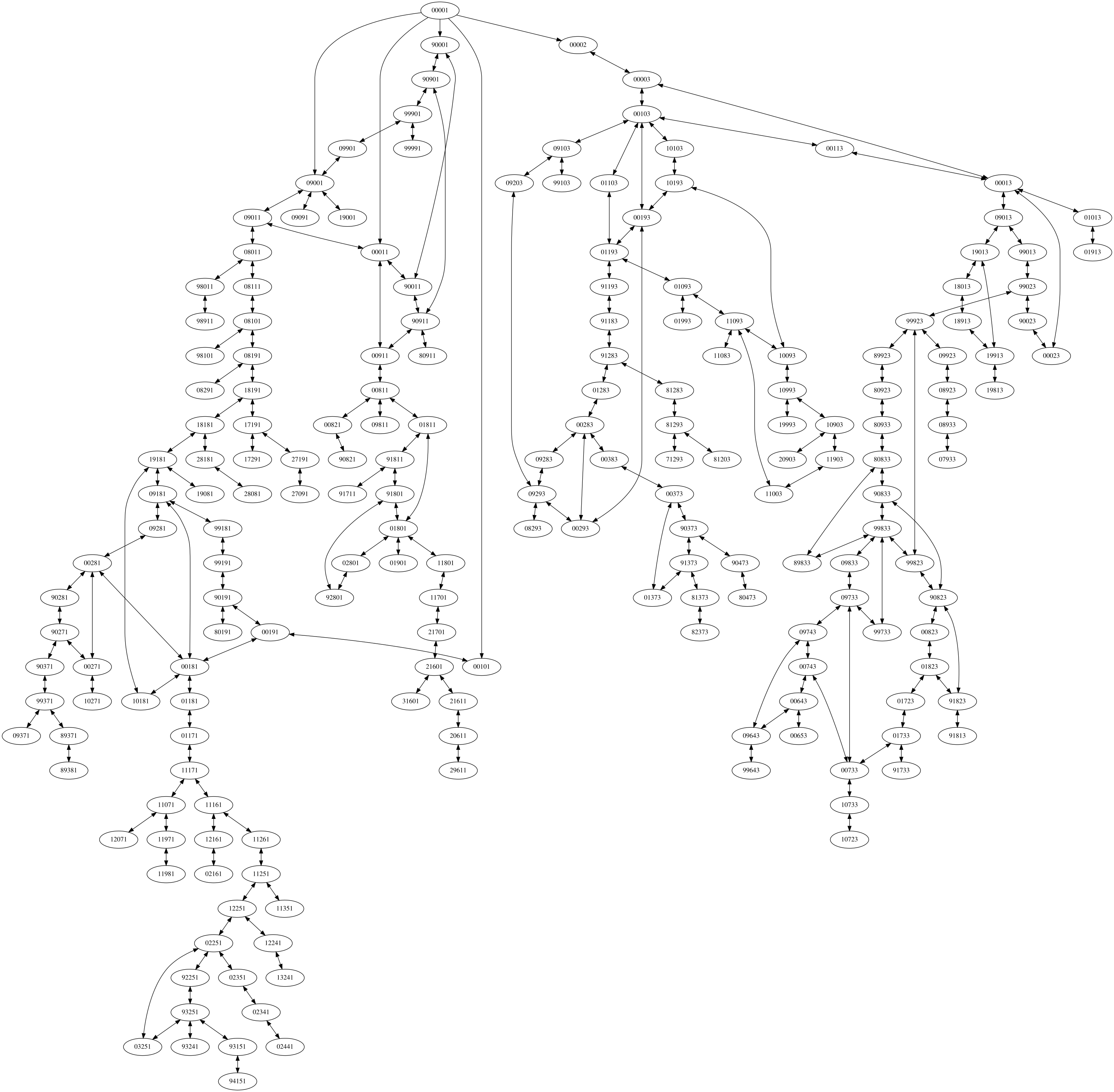
A map

Here's a map of the entire search space, generated with graphviz:

(Click to view large SVG - I suggest zoom out to a level that fits the entire thing on the screen at once)

00001 is at the top and 10723 is the lowest point on the right-hand side.

(I've omitted the arrows that point from every node to 00001.)

The puzzle about the combination lock is isomorphic to pathfinding from 00001 to 10723 on this graph.

I think the graph is small enough (and is laid out sensibly enough) that manual pathfinding is doable, however I think creating the graph by hand would be too much trouble, so I don't think the puzzle is readily solvable by hand in a sensible amount of time.

Mandatory move to 00013?

We already have a proof that it is mandatory to pass through 00003. From looking at the map it is easy to see that it is also mandatory to pass through 00013 if you want to access the subgraph that leads to 10723.

Is there a reasonably straightforward argument that the route must pass through 00013 (along the lines of the argument about 00003) or is it just a very lengthy process of elimination?

Why start on 00001?

I originally wanted to start the combination on 00000, but it took me far too long to realise that there are no legal moves. 00001 is the next obvious choice.

It is kind of unpleasant that 00001 is the sole reachable state that is not prime, but if the start state were 00002 instead then the entire left half of the search space (as shown in the map) would be unreachable. I prefer it this way.

Adventure game

We could imagine using the map to create a text adventure. The simplest way is to just make an ordinary game and connect up the map of the game in the same way as the graph of Prime Combination. Compare to A treasury of Zork maps.

But we can view the digits of the nodes as integer coordinates in a 10x10x10x10x10 5-dimensional hypercube (or, a 5-dimensional hypertorus, since the edges wrap) and then the game is maybe to work out the general rule that decides which movements are legal?

Or maybe you spawn at a random place in the map and you have to work out where you are, without knowing your coordinates, based only on moving around and noting which passageways are open?

Big map

I have a much bigger map of the entire space of prime connections. It includes the isolated subgraphs that can't be reached from 00001. It's at https://incoherency.co.uk/interest/prime-combination-big.svg (warning: 5 megabyte SVG, may lag your comp - I suggest zoom out to a sensible level and then scroll horizontally).

This map contains 2735 separate connected components of 2 or more nodes. There are also 8402 individual primes not shown, which aren't connected to any others. Of the 2735 components, 450 only contain 2 nodes. There are 172 that have more than 10 nodes.