Optimal eccentric-weighted coins

Thu 12 January 2023
Tagged: science

If you wanted to make a hole in a coin so that the centre of mass is moved as far away from the original centre as possible, how big a hole would you make and where would you put it?

This is quite reminiscent of the "Centre of mass of a soda can" problem, which asks how the centre of mass of a can of drink changes as the drink is consumed. (You might enjoy giving it some thought if you haven't seen the problem before).

Wall thickness

We want the outer circumference of the coin to be retained, which means we can't drill the hole right at the edge. We need some minimum wall thickness, otherwise we don't have a coin any more, we have more of a crescent moon.

Limit cases

The limit cases are:

1.) 0-sized hole: we can trivially see that this does not affect the mass at all, the centre of which remains in the centre.

2.) Maximum-sized hole: this leaves us with a symmetrical ring, with the centre of mass also in the centre.

Hole locations

We can also see that for any size of hole, if the hole does not touch the perimeter (modulo the minimum wall thickness), then we can produce a corresponding coin with the same-sized hole, where the hole does touch the perimeter, and this second coin will have a more eccentric centre of mass than the first.

Maths

So for a given coin radius (r_coin) and minimum wall thickness (w), we only have one variable: the radius of the hole (r_hole). We'll work with radii instead of diameters because it makes the maths easier.

Since we're looking at a 2-dimensional cross section, the mass of the coin is proportional to the area of the shape in cross section.

So the mass of the original coin is proportional to its area, m_coin = πr_coin².

The mass removed when we drilled the hole is proportional to the hole's area, m_hole = πr_hole².

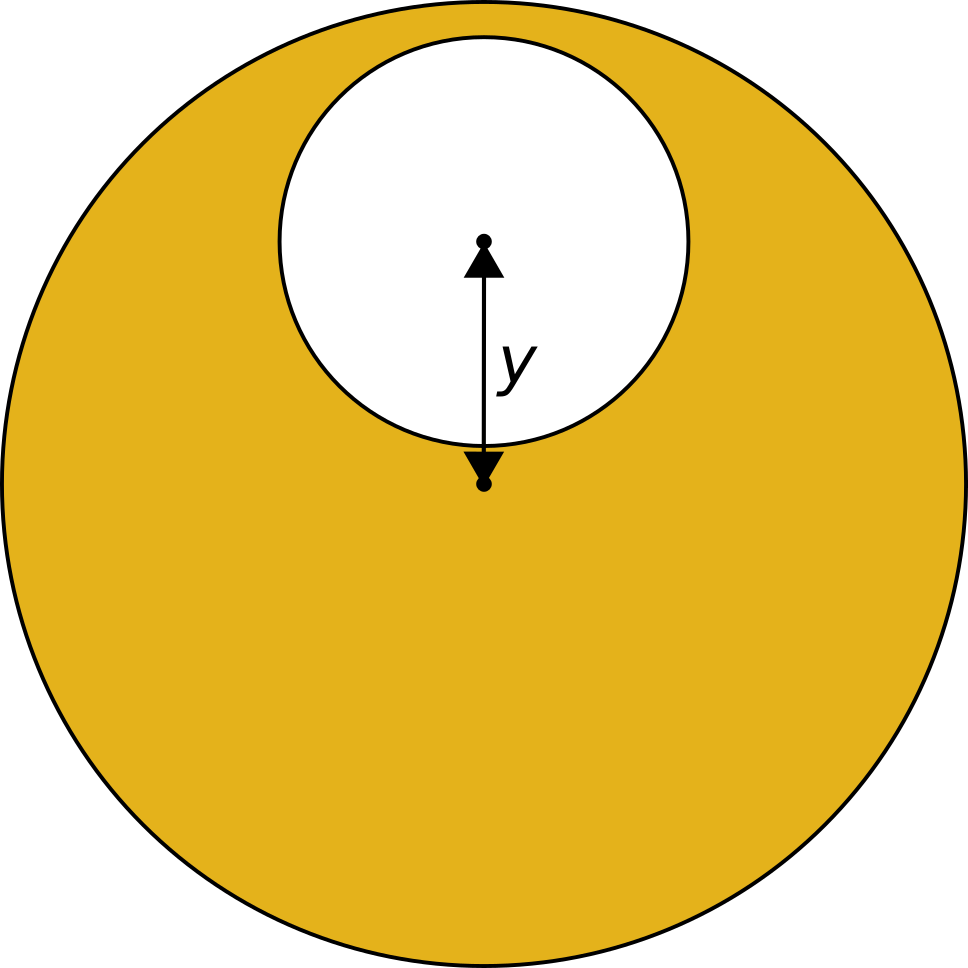
To leave a gap of w between the circumference of the hole and the circumference of the coin, y = r_coin - r_hole - w.

And to work out where the resulting centre of mass lies, we'll say the coin is a body at the origin, with a mass of m_coin, and we'll say the hole is a second body with (negative) mass -m_hole, positioned with its centre at a distance of y away from the centre of the coin.

Weighting the mass of the hole by its location, the radial position of the centre of mass is therefore r_mass = m_hole * y / (m_coin - m_hole)

So r_mass = πr_hole² * (r_coin - r_hole - w) / (πr_coin² - πr_hole²) = r_hole² * (r_coin - r_hole - w) / (r_coin² - r_hole²).

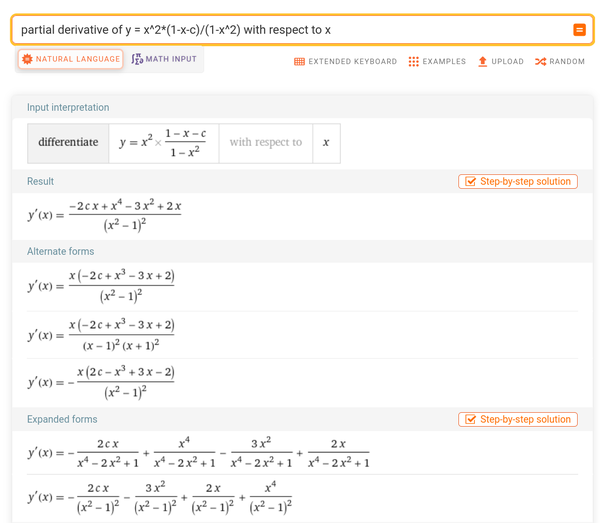
To work out where r_mass is maximised, we can find the partial derivative of this function with respect to r_hole and solve r_mass' = 0.

...at least, that was the plan, but differentiating that function proved too inconvenient.

So let's lose a variable: scale everything so that it's proportional to r_coin. Now we have:

R_coin = 1
R_hole = r_hole / r_coin
W = w / r_coin
r_mass = R_mass * r_coin
R_mass = R_hole² * (1 - R_hole - W) / (1 - R_hole²)

This is still too difficult for me to differentiate by hand. With variable names substituted for single letters, WolframAlpha gives:

and

Which is... not what I was hoping for. Did I make a mistake?

Charts

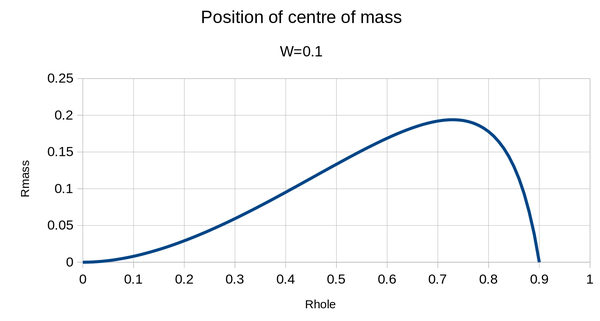
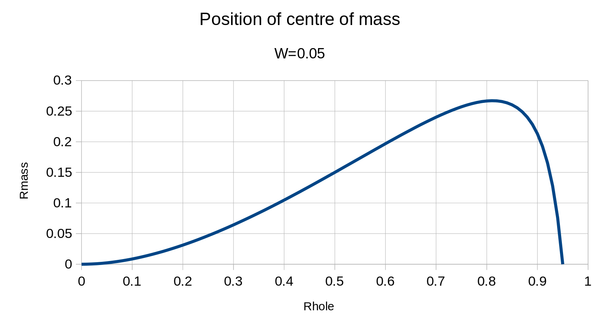
I gave up on trying to find a closed-form solution at this point and brute-forced it with a spreadsheet, for W=0.1:

When the minimum wall thickness is 10% of the radius of the coin, the optimum eccentricity (with centre of mass almost 20% out from the centre) is achieved when the radius of the hole is about 73% of the radius of the coin, which looks about like this:

That's a much bigger hole than I expected! That's why it's important to calculate these things rather than guessing. Looking at the shape of the chart, we also see that if there is likely to be some error in the size of the hole, it's best to err on the side of making the hole too small than too large.

W=0.1 corresponds to a 1mm wall thickness on a 20mm diameter (10mm radius) coin, which I think is pretty reasonable. But how much is that limiting us? How much better does our eccentricity get if we allow a slightly smaller wall thickness?

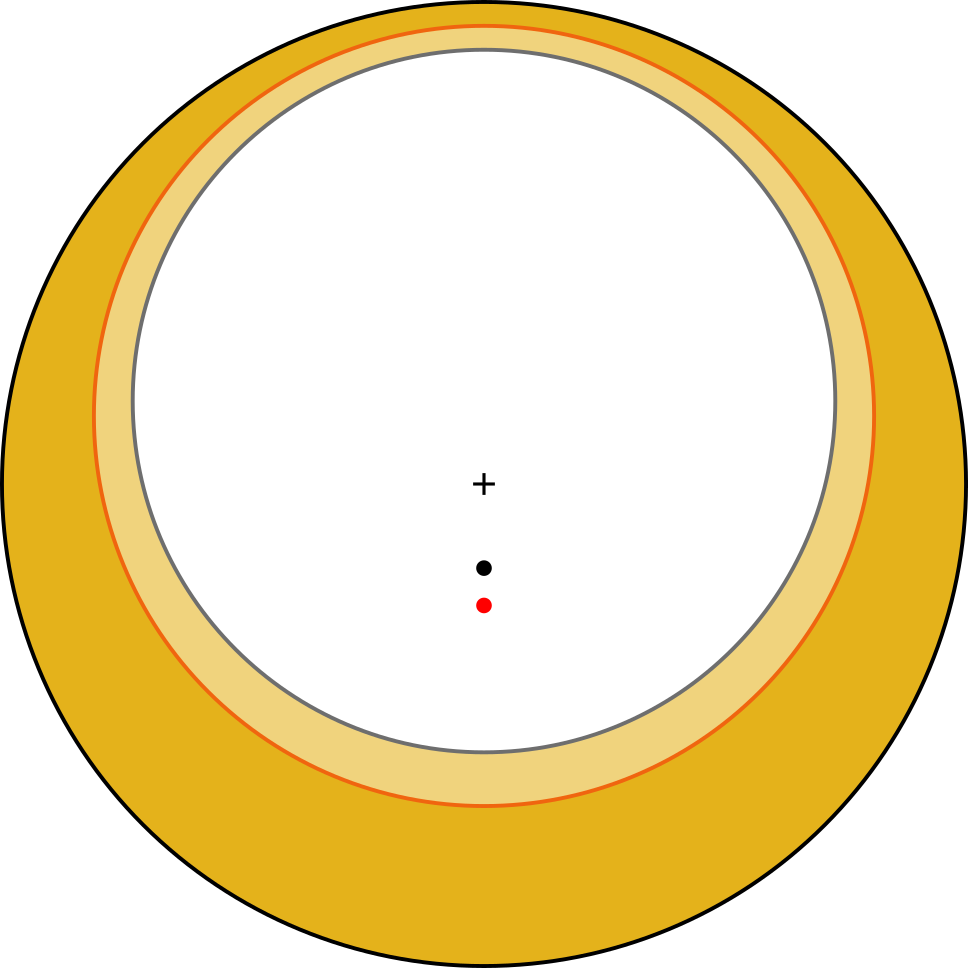
Centre of mass now almost 27% out from the centre, or about 35% better. And here are the two implied optimal coins, overlaid, and with centres of mass marked:

(W=0.1 in black, W=0.05 in red, "+" marks centre of original coin, dots mark centres of mass)

Conclusions

1.) Always position the hole as close to the edge as possible.

2.) For a 1mm wall on a 20mm coin, drill a ~14.5mm hole. The resulting centre of mass will be about 2mm away from the centre point of the coin.

3.) For a 0.5mm wall on a 20mm coin, drill a ~16mm hole. The resulting centre of mass will be about 2.6mm away from the centre point of the coin.

If you like my blog, please consider subscribing to the RSS feed or the mailing list:

Subscribe