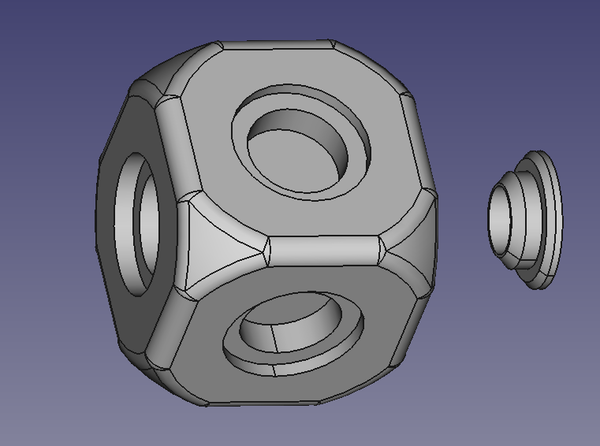
I've put together a physical version of the magnetic cubes puzzle and have spent a good few hours playing with it. (You don't need to have read that post in order for this one to make sense, but it might help, and it's certainly worth having a look at the table that labels the different cube configurations). I haven't yet managed to solve it without consulting a computer.
(It's sitting in a Tiny Rubik's Cube Stand designed by Stephen Lai).
Building it
I recently acquired a new 3D printer. It's an "Anycubic i3 Mega" that I bought directly from China for £289. The print quality is substantially better than the cheaper machine I bought last year. I'm very pleased with the Anycubic.
My original plan was to 3D print cubes with hollow spaces just underneath each face, and then drop in magnets mid-print to finish up with solid cubes with embedded magnets. Unfortunately, despite the fact that the nozzle is brass and the heater block is aluminium, the hot end seems to have some steel in it, and on my first test cube the magnet jumped up out of its hole and stuck to the hot end. So that wasn't going to work.
My next plan was to 3D print cubes with indentations in the faces that I could then superglue magnets in to. I superglued one magnet into one cube as a test, determined that it would work, and then printed the rest of the cubes (~13 hours of 3D printer time). When I came to glue more magnets in I found it very difficult to hold the magnets in place without opposing poles in the centre of the cube causing the magnets to flip over, or jump out of place and stick together, before the glue had dried. I gave this quite a good go but I just couldn't get it to work.
Finally I 3D printed cubes with "stepped" indentations in the faces, and I 3D printed little plugs to fit in the indentations. I glued a magnet into each plug and then glued the plugs into the faces. This made the magnets easier to handle and less prone to flipping over. This worked much better. Another benefit of this method is that I can use a different-coloured plastic for the plugs so that I get the faces coloured for no extra effort.
Then it's just a case of gluing 162 magnets into 162 plugs, and then gluing 162 plugs into 162 faces.
Jez suggested sticking the cubes together with velcro instead of magnets. This would be a lot easier to make as you wouldn't have to worry about unwanted interactions between magnets.
Solving it
I found it very easy to assemble the cubes into a 3x3x3 if you don't care what the outside faces look like. Just pick cubes at random until you find one that fits, and if you run out of options, remove some cubes at random and try again. I only needed to backtrack 2 or 3 times to find solutions.
With the condition that the outside faces have consistent colours, it is extremely difficult to assemble the cube, and I haven't managed to do it without looking at a computer-generated solution (of which there are many, many possibilities; I stopped counting them after 100 million, but I'm interested in placing some bounds on what the exact number could be, please email me if you have any insights).
I did come across a few observations that are useful in reasoning about the cubes.
1. Some cubes can only go in certain locations
This seems obvious in hindsight, but is actually quite helpful. For example, the 2 cubes that have 6 green faces can only go in 8 of the 27 possible locations. And since they both have all-green faces, they can't be touching each other. Similarly, the 2 cubes that have 6 red faces can only go in 8 of the 27 possible locations, and can't be touching each other.
There are 7 locations in the cube that have 2 adjacent green faces on display, so the cubes that don't have 2 adjacent green faces (if green is South, these are: 6N, 1S, 2So) can't possibly go in those locations, and the same for red (6S, 1N, 2No), on the opposite edges of the cube.
2. You can sometimes disprove solvability of a partial cube without exhaustively searching
Let's say we've assembled the first 2 layers of the cube, and we've got 9 pieces left to place. For sake of argument, let's say we need to have all red faces on top. If we have any cubes that don't have any red faces (6S) then we know immediately that this state is not solvable, and we must backtrack and try again with the 2nd layer.
If we have any cubes that have only 1 red face (1N) then we know that they can be placed in only 4 of the 9 possible locations on the top layer (the red face must face upwards, and the piece can't go in any of the 5 locations that also require a red face to be showing on the side). Furthermore, since the piece must have a green face facing down, it must be placed on top of a piece from the 2nd layer that has a red face on top. If there are no red faces on top of the 2nd layer in the 4 allowable positions, then we know this state is not solvable, and we must backtrack and try again with the 2nd layer.
You can follow as many of these logical arguments as possible until you either disprove solvability, or find a piece that can only be placed in one location. After placing it, follow similar logic with the remaining pieces, with the added constraint that they must be able to fit next to the pieces that have already been placed.
But we still need a way to place pieces in the lower layers that is better than guessing. I haven't come up with anything for that.
3. Thinking about the faces independently
It can be instructive to think about the faces independently from the cubes to which they're attached. If we can disprove solvability of a set of faces, then we don't need to care how those faces are arranged into cubes as they won't be solvable regardless.
All of the individual faces end up either visible or non-visible when assembled into a 3x3x3. The non-visible faces are non-visible because they're inside the cube, and adjacent to another non-visible face, of the opposing polarity. That means exactly half of the non-visible faces are red, and exactly half are green, otherwise it would not be solvable. So we need to have at least 6*9=54 red and 54 green faces just in order to be able to assemble the cubes into a 3x3x3.
This doesn't actually help us with the cube set I've made, since there are exactly 81 red and 81 green faces, but it helps to rule out certain outer-face patterns as impossible.
A solution
Here's one of the solutions I generated.
Red is North and green is South. The outside cells are labelled with just a colour to show what colour should be facing in that direction (green left and top, red right and bottom), and the cells representing individual cubes are labelled with the colour that should be facing upwards. The bottom layer is given first (and must have green faces facing down), then the middle layer is given, and then the top layer.
| 6S | 1N | 2No | ||||
| 3C | 3R | 3C | ||||
| 1N | 2So | 3C | ||||
| 2No | 2Sa | 2Sa | ||||
| 2Na | 6S | 2So | ||||
| 2So | 2Sa | 6N | ||||
| 1N | 1S | 2Na | ||||
| 1S | 2No | 1S | ||||
| 2Na | 6N | 3R | ||||
Probably doesn't make much sense on its own, but if you have a set of cubes in front of you, it'll help. I swear.
For example, consider the 3C on the left of the middle row of the first layer. We know it needs to have a green face facing down because it's the first layer. We know it needs to have a green face facing left because all of the left-most faces have to be green. We know it needs to have a red face facing up because the cell is shaded red. That's enough information to know how to place the cube. I think some of the squares are actually ambiguous, but they become non-ambiguous if you just skip them and place the surrounding cubes first.
Anyway, I think that's about all I've got to say about the cubes for now, aside from the answers to the questions from the end of the last post. If you make a set of cubes or have any insights into how they might be solved please get in touch.
Exercise solutions
1. Is it possible to choose a cube set that is impossible to assemble into a 3x3x3 cube?
Yes. A trivial example is 27 6N cubes. You can't assemble 2 6N cubes together in any orientation, so it's obviously impossible to assemble 27 of them together. More interestingly (as discussed above), any set of cubes which has fewer than 54 red or fewer than 54 green faces can not be assembled into a 3x3x3.
2. Is it possible to assemble the cube set given above (2x 6N, 2x 6S, 2x 3R, 3 each of the rest) into a 3x3x3 cube of cubes that has the same colour on every outside face?
No. We always need to have 54 red and 54 green faces in the non-visible parts of the cube. If we want all of the outer faces to be red, we need all 54 of the outer faces to be red as well, for 108 red faces in total. Since our cube set has only 81 red faces and 81 green faces, it is impossible to assemble into a 3x3x3 that has the same colour on every outside face.
3. Is it possible to choose a cube set that can be arranged in to both a checkerboard pattern and a consistent-faces pattern?
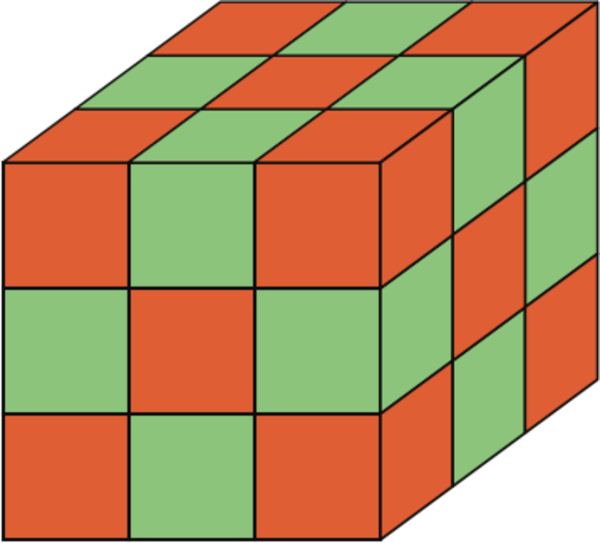
No. Consider the checkerboard image I mentioned last time:
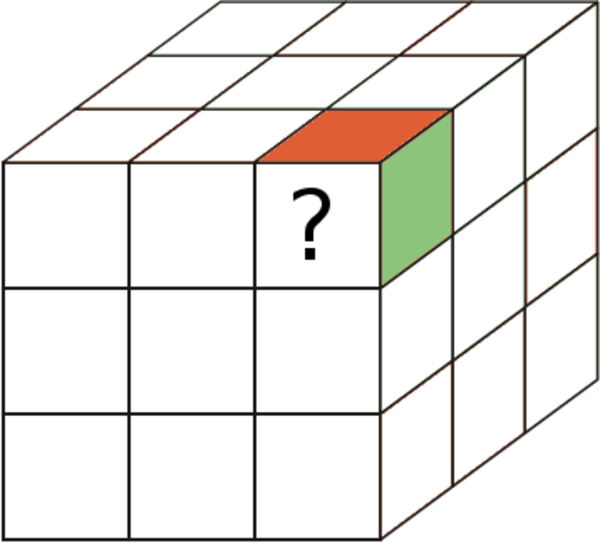
You'll note that the edges of the cube don't seem to follow the checkerboard pattern as applied to individual faces. The reason is that on each of the corners we find a square where we can place neither red nor green without breaking the pattern:
Therefore the only checkerboard pattern that can actually make sense on a cube is a checkerboard of cubes, rather than faces.
You'll also note that each face has 5 red faces showing and only 4 green faces showing, for a total of 6*5=30 red faces and 6*4=24 green faces. We know that both a checkerboard pattern and a consistent-faces pattern have exactly 54 red and 54 green squares in the non-visible part of the cubes. So we need to decide if it is possible to create a consistent-faces pattern that uses 30 red faces and 24 green faces, and the answer is no.
If we want 3 red 3x3 faces and 3 green 3x3 faces, we need 27 of red and 27 of green, which isn't enough reds. If we make a concession for extra red faces and go for 4 red and 2 green sides, we need 36 red and 18 green faces, which is too many reds and not enough greens.
Therefore it is not possible for any cube set that can form a checkerboard pattern to also form any consistent-faces pattern.