A short pendulum with a long period

The period of a pendulum is proportional to the square root of its length: to double the period, the pendulum needs to become 4x as long. But actually physics has no idea how long your pendulum is, the thing that really matters is the radius of the arc that the centre of mass travels through. There's no inherent reason that we wouldn't be able to increase the radius of this arc without increasing the height of the pendulum.

Demo

Here's a quick-and-dirty Matter.js demo of the simplest mechanism I could think of:

If it runs out of energy you can refresh the page or give it a kick with your mouse.

The pendulum on the left is a "normal" pendulum. The one on the right has a linkage that makes the effective pivot point of the pendulum swing left and right with the weight. This has the effect of flattening out the path of the weight, which approximates an arc of greater radius.

I had to "cheat" in the demo because I couldn't work out how to use Matter.js constraints to keep the angles of the short and long arm synchronised. The pivot at the top is actually static as far as Matter.js is concerned, and my code manually updates its position. This is why the green line has some slight deviations.

How it could work in real life

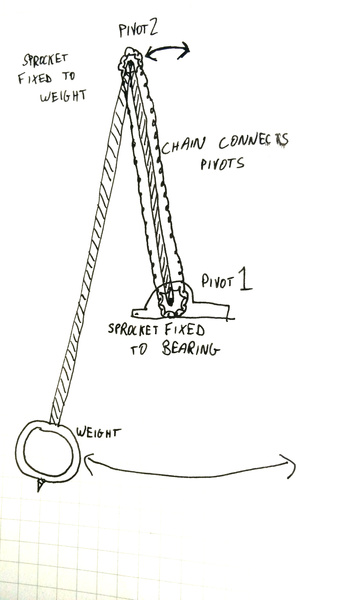
I wasn't clever enough to include a representation of the actual linkage in the animation, but I envisage something like this, where there is a sprocket at each end of the short arm, with a chain that keeps the angles synchronised:

The sprocket at "pivot 1" is fixed to the frame of the apparatus, and the sprocket at "pivot 2" is fixed to the long arm, so that as the long arm rotates, "pivot 2" pulls itself around the chain, which rotates the short arm around "pivot 1" because the sprocket at "pivot 1" can't move.

If you spend some time thinking about it you might undertand it. Instead of a chain and sprockets we could just as easily have a gear train with an odd number of gears, or a pair of pulleys with a string fixed at opposite sides, or possibly something even better.

Why it's good

I have a vague idea that I'd like to build a mechanical clock at some point. I'm kind of thinking a floor-standing clock of grandfather clock scale, but with less fine woodworking, and more exposed workings of unusual design.

I think it would be fun if the clock ticked really slowly and purposefully, with the second hand jumping several seconds with every tick. To achieve this with a standard pendulum, the clock would need to be very tall indeed. If the clock ticks twice per period of the pendulum (once for each direction), then to get a tick every 5 seconds you would need a 10-second period, which implies a pendulum that is 25 metres tall, which is clearly absurd.

Why it's bad

It is probably very difficult to build the two-armed-linkage with sufficiently-low friction that it would actually work in a clock. I don't know how much energy an escapement can typically impart into a pendulum with each tick, but it is presumably low, otherwise it would compromise the pendulum's regularity (maybe?).

More importantly, the fact that the two-armed-linkage pendulum does not swing through a true circular path means that its period is not truly constant. The mean radius decreases as the weight swings higher, which presumably means the period decreases as the weight swings higher. To get a constant period out of this pendulum, you'd need to ensure that it swings to the same height on every stroke, and if you can do that then you don't need a pendulum in the first place.

My thinking is that the period won't vary too much throughout the useful range of the pendulum, and it doesn't matter if the clock drifts a bit anyway. It would be good to do some calculations to quantify how the period changes with the swinging height. But I can't immediately see how to do that.

Parameters

A normal ideal (spherical cow, frictionless vacuum, etc.) pendulum only has 1 parameter: the length. Or, more precisely, the radius of the arc that the centre of mass swings through.

Our two-armed-linkage pendulum has three interesting parameters: the length of the long arm, the ratio of the length of the short arm to the long arm, and the gear ratio of the sprockets.

As the short arm length tends towards 0, the motion of the two-armed-linkage pendulum tends towards that of the classical pendulum. As the short arm length tends towards that of the long arm, the "arc" tends towards a straight line, where gravity will no longer have any effect on the weight. Where the "short arm" is longer than the "long arm", I think the arc is inverted and gravity will pull the weight towards whichever side it is already on, rather than always pulling towards the centre.

It's not immediately clear to me what happens as the gear ratio changes. My demo and sketch assume a 1:1 ratio, but it is possible that there is a better choice which would more faithfully approximate a circular arc.