Secrets of the Hanayama Cast Marble
Wed 8 July 2020Tagged: puzzle, 3dprinting
Cast Marble is a mechanical puzzle sold by Hanayama. It was invented by Bram Cohen (who you may recognise as the inventor of BitTorrent) and Oskar van Deventer, who has an interesting YouTube channel where he regularly posts new puzzle designs.
The puzzle is made of 4 parts, which are 2 identical copies of 2 types of part. 2 of the parts form a ball in the centre, and the other 2 form a box around the outside. The goal is to separate all of the parts.
(Spoiler alert: this post is intended to reveal the working principles of this puzzle to an even greater extent than you are likely to have discovered by merely solving it. Don't read on if you still want to solve the puzzle yourself. Remember that "knowing the solution cannot be reversed".)
Solution
The solution is quite simple, although very hard to discover. You need to align the cut line on the ball with the cut lines on the outer box, and then twist the whole thing apart. After half a rotation, the parts have drifted apart sideways and can then be separated easily.
This seems a bit like half a turn on a screw thread, but unlike a screw thread it is composed of 2 identical halves, rather than a male thread and a female thread. I initially thought that the centre of rotation of each part was inside the other part, but actually they share a common centre of rotation, and it is a simple helix.
Geometry
This animation shows what we get by sweeping a rectangular profile through a helical path:
If the centre line of the rectangular profile is collinear with the central axis, and the height of the rectangle is half the pitch of the helix, then a length of the resulting shape takes up exactly half the volume of its bounding cylinder, and 2 copies of it will thread together to form a solid cylinder without overlapping each other. This isn't just a trick of computer graphics, it works in real life:
I don't know if this kind of shape has a name, I couldn't find one, but might not have known the right search terms. I like to think of it as a "hermaphroditic screw thread". It might be funny to make some real hermaphroditic screws, with proper screw heads, and use them to bolt stuff together.
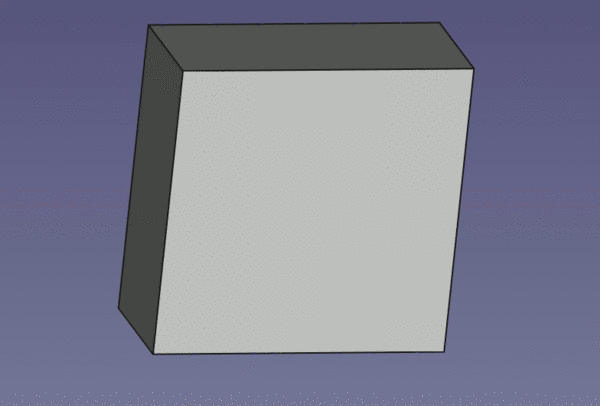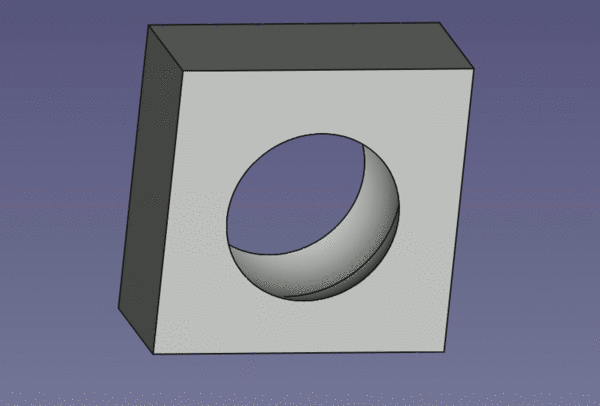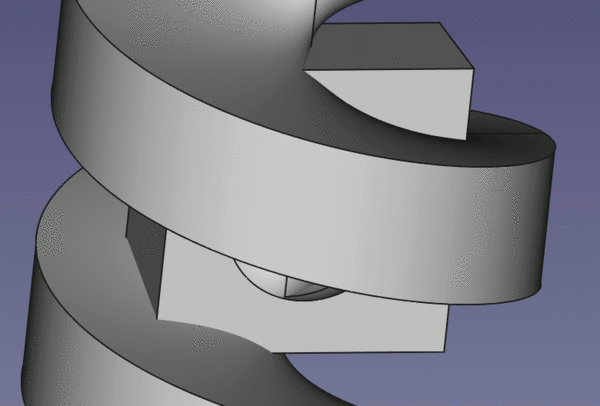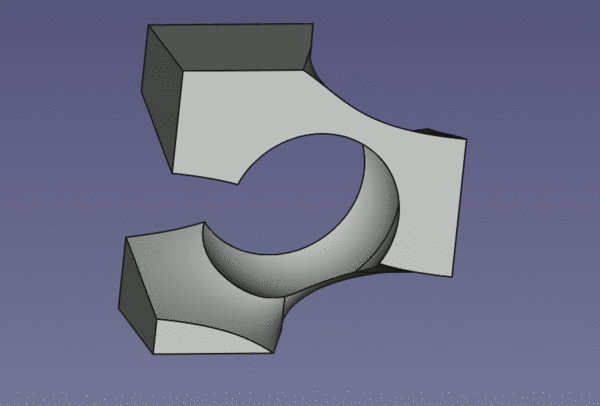
This photograph shows how the puzzle parts share the hermaphroditic screw geometry:
And we now see that the apparently complex surfaces of the puzzle parts are formed from just a few primitive shapes!
Reproduction
I was surprised to find that the Hanayama Cast Marble uses a left-handed thread on its hermaphroditic screw. I'm not sure whether this makes the puzzle easier to hold for a right-handed person, or harder to solve because people aren't used to left-handed screw threads.
I measured the thread pitch by twisting the puzzle through half a turn and measuring the offset between the box parts, which was about 18 mm. We then know that the thread pitch is twice this much, so the thread pitch is 36 mm. It's a bit of a crude measurement but I think I got it right. It's close enough that the parts fit together, anyway.
Once we understand this much, the design of the puzzle is mostly straightforward with CSG modelling.
The ball parts are made by intersecting a sphere with the hermaphroditic screw.
And the box parts are made by subtracting a sphere from a cuboid and then intersecting the result with the hermaphroditic screw.
If you want to print your own copy, you can download the STL files.
The parts created this way are mostly interchangeable with the original puzzle parts:
Although the printed box is not quite symmetrical, because I obviously cut it from the wrong place in the thread:
Rounded edge
Having put the printed puzzle together, I discovered one extra trick up the Cast Marble's sleeve!
Part of the reason the Cast Marble is so difficult to solve is because the box parts can rotate around the centre in a way that is not used in the solution:
This is due to a rounded edge on the box parts, which does not naturally occur from the basic shape of the puzzle:
More
An interesting property of the hermaphroditic thread is that any 2 threads will fit together, provided they have the same pitch and profile, regardless of their diameter!
This means we could use the hermaphroditic thread to cut anything into 2 parts in a way that allows them to thread together. I tried to do this with a few models I found on Thingiverse but they had quite a lot of triangles, and FreeCAD exhausted my machine's available RAM and crashed before it completed the intersection. In principle it would work though.
In addition to extending up/down to infinity, we can also extend our helix outwards (radially) to infinity. This leads to 2 identical half-universes that can be screwed together, which is quite a bizarre concept to wrap your head around. It's surprising that it's even possible. I would be interested to learn of any other ways of splitting an infinite space into 2 identical halves that can move but also constrain each other, because they might lead to low-hanging fruit for new puzzle designs.
It might be interesting to experiment with alternative thread profiles. You need the inner edge to be a straight line segment collinear with the central axis, but there's no reason that the upper and lower edges of the profile need to be straight. They can be whatever you want as long as they match:
If you like my blog, please consider subscribing to the RSS feed or the mailing list: