Flat Earth and the Coriolis Force

I've been learning about "flat-Earthers" recently. They're a fascinating group of people who genuinely believe that the Earth is flat and that governments, scientists, and industry are in on a big conspiracy to trick everyone into thinking the Earth is round.

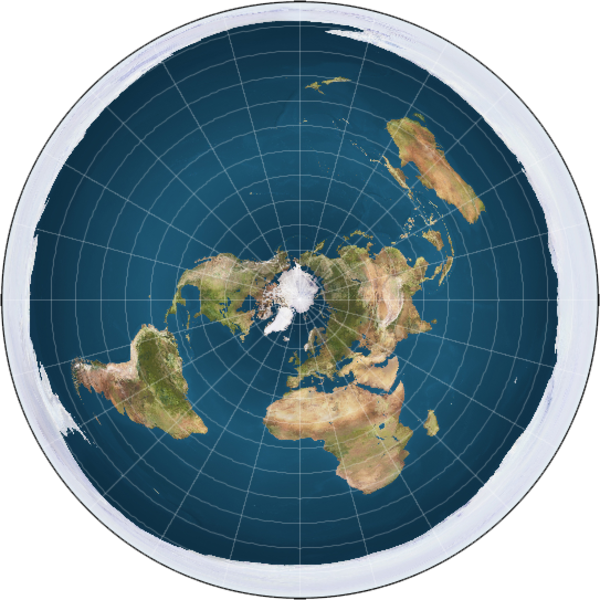
Flat Earth

Mostly the flat Earth arguments are derived from a fundamental misunderstanding of gravity, leading to statements like "any body of water always sits level, so how can the seas curve around the Earth?" and "a railway from east to west coast of the UK would have to rise so far up in the middle that no train would be able to make the climb". There is also extrapolation of an "8 inches of curvature per mile squared" surveying rule-of-thumb well beyond its useful range, references to passages from religious texts, and observations that photos of things taken in space look funny. There is a widespread belief (among the flat Earth community) that all space travel is fake. It really is fascinating to look into. But make sure you go in with either a good grasp of how gravity works, or a healthy dose of epistemic learned helplessness, else you might turn into One Of Them.

(Incidentally, "epistemic learned helplessness" is a really interesting concept, I recommend reading the essay. It's about the idea that most people are better off just going with whatever is most popular, rather than listening to reason, because they lack the skills to correctly evaluate ideas, and are more likely to be misled by bad ideas than to be misled by copying the popular idea).

A lot of the YouTube comments on flat-Earth videos are from round-Earthers trying to show that the video is wrong. Obviously the video is wrong, but what I find really interesting is that many of the round-Earthers are wrong about why the video is wrong! Ideas like "the laser is visible on the other side of the lake because the laser is bent down by gravity", or "the reason a hammer and a feather accelerate downwards at the same rate is because their masses are quite close to each other relative to the Earth". Flawed debunking of the flat-Earth concepts probably contributes to why the flat-Earthers continue to believe their concepts: they keep seeing wrong arguments for why the Earth is round, so the Earth must not be round. (Although, even if the arguments were right, "one can't be reasoned out of a position that one wasn't reasoned into").

Foucault's Pendulum

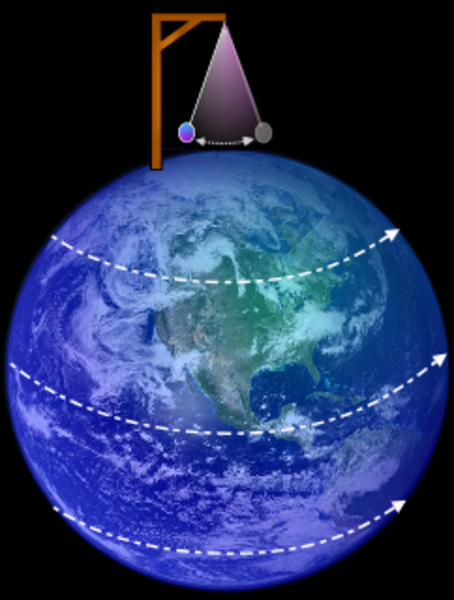
An interesting experiment that shows that the Earth is rotating is Foucault's Pendulum. This is just a large pendulum whose motion can be observed. The weight on the pendulum has inertia, and the pendulum is mounted on a rotating body (the Earth). The pendulum "wants" to keep swinging in the same direction, but our reference points (buildings, trees, etc.) for that direction are all fixed to the Earth, and therefore our reference points are rotating relative to the pendulum. If we assume the reference points are not rotating, it appears as though the motion of the pendulum is rotating.

Foucault's Pendulum is also consistent with the Earth being round, because the magnitude of the effect decreases as you move from the North pole to the equator (at which there is no effect, because at the equator the pendulum is perpendicular to the Earth's rotation axis), and then reverses, and increases in magnitude as you move from the equator to the South pole.

Coriolis Force

The rotation of the oscillation of Foucault's Pendulum is described by the Coriolis Force. The Coriolis force is not a "real" force (in the same way that the centrifugal force is not a "real" force), it is just a force that appears to exist when an object is measured from within a rotating reference frame. When turning left in a car, you feel yourself being pushed right, towards the outside of the turn, by the "centrifugal force". You're not actually being pushed towards the outside of the turn, you're just an object moving in a straight line (Newton's first law) while the car moves left.

Similarly, the Coriolis force is not actually rotating Foucault's pendulum. The mass on the end of the pendulum is just an object moving in a straight line (ish) while the Earth rotates underneath it. Once this is understood, the Coriolis force needs no explanation at all. It is a natural consequence of Newton's laws of motion on an object that is observed from a rotating reference frame. This might seem obvious to you, but I didn't get it until I'd thought about it for a little while.

Throwing a ball on a spinning disc

While thinking about the Coriolis force it occurred to me that if you were sitting on a spinning disc, and you threw a ball straight towards the centre of the disc, you might be able to catch it again on the other side if the disc is spinning fast enough. I looked for some examples of people actually doing this, and couldn't find any. I did find a couple of videos that demonstrated the effect, but failed to make the connection that the ball could be returned to the thrower. In addition, they both made the same mistake. The people on the spinning disc made no effort to cancel out their own velocity from the initial velocity of the ball. They throw the ball directly forwards from where they're sitting, but since they are moving around the disc, they already have some velocity tangent to the disc. A ball that was truly thrown in a straight line across the centre of the disc would pass over the centre point of the disc, but the balls in those videos do not.

I did find one example in which the ball is returned to the thrower. At about 0:14, the red person sits on the disc and rolls a ball out to the side, cancelling out the tangential velocity, and waits for the ball to curve around and come back. Unfortunately, since the ball was rolled across the disc instead of thrown through the air, this too has a mistake. Consider a ball which is placed stationary on the disc: the centrifugal force would cause it to move towards the outside, with no Coriolis force required at all!

Javascript simulation

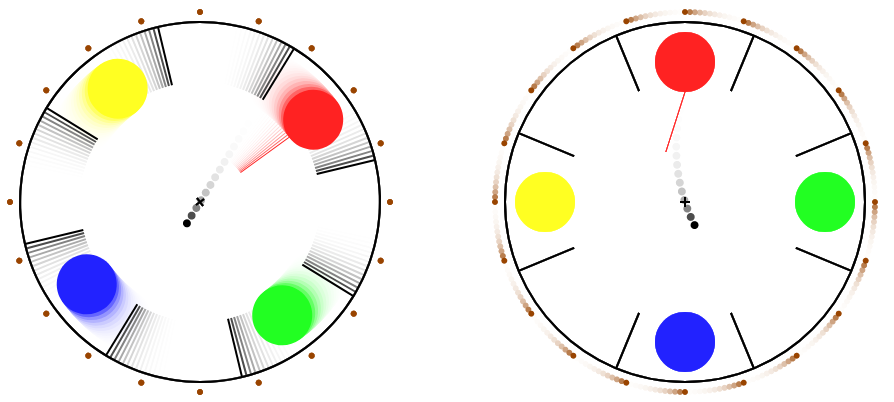
Since YouTube University wasn't delivering the goods, I made my own demonstration in Javascript. You can play with it here:

We have two views of the same scene. The left view is fixed in space, and the right view rotates with the disc so that the disc appears to be still. There are 4 coloured dots on a spinning disc, and a ball can be thrown from the red dot. The brown dots around the outside are fixed in space as reference points. On the view that is rotating with the disc (in which the disc appears to be still and the brown dots appear to be moving), the thrown ball appears to travel through a curved path even though no force is acting on it. This "phantom" force is the Coriolis force. I did not actually implement any calculations for the Coriolis force. I simply simulated the movement in an inertial reference frame, and the Coriolis effect appears naturally when the scene is observed from a rotating reference frame.

If the tangential velocity is cancelled out (e.g. by setting V_x to -0.64 m/s, at 10 rpm in the simulation), then the ball travels directly through the centre of the disc. To an observer who is rotating with the disc, the ball appears to have been thrown off to one side, before swinging around and passing through the centre.

Having spent some time playing with this, I remembered the timeless "Tanks" game:

Each player has a tank on a hillside, and has to try to shoot a bullet at the other players' tanks, by adjusting the gun angle and firepower. Gravity acts on the projectile so that it travels in a parabola.

Wouldn't it be fun to play a similar game, except instead of a hillside with gravity, the tanks are positioned around the edge of a spinning disc? You can play with that as well. It starts out slow, so the Coriolis effect is small, and speeds up with each level.

The radial lines around the edge of the disc actually provide collision detection. Originally they did not, and the winning strategy was to simply point your gun opposite to the direction of rotation, and then adjust the firepower so that the tangential velocity is cancelled out. This causes the bullet to remain fixed in space, and then you just wait for the disc to rotate around until your opponent crashes into your bullet.

Anyway, as it turns out: no, it's not very fun.