Advent of Code on my homemade CPU
Fri 31 December 2021Tagged: software, cpu
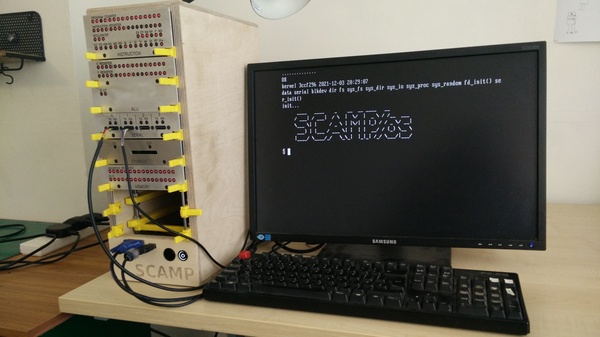
This year I've built a 16-bit CPU, along with custom operating system and programming language. It runs at 1 MHz and has 64 KWords of memory. This December I used it to do Advent of Code.
This is what it looks like:
It's relatively common to write Advent of Code solutions to run on limited hardware. What isn't so common is to develop on the limited hardware, which is what I've been doing, even to the point of reading the problem statements and submitting the solutions via a proxy running at the other end of a serial port. The main difference is that exploratory programming is much more difficult in an environment where you can't just write a quick Perl script to learn something about the shape of the problem. Even compiling a small program takes over a minute.
So far I've completed part 1 of every day except day 24, and part 2 of every day except 15, 22, 23, and 24, although on a couple of days I did resort to using the emulator (~20x faster) when the physical hardware got too frustrating.
Videos
I recorded video of a lot of my attempts. I think the day 6 video is a good one to start on, because it is relatively short and easy to understand, and I didn't make too many blunders. You might still prefer to watch on 1.5x speed.
I enjoyed doing the videos, and a handful of people told me they enjoyed watching them, so I think I'd like to do more programming videos in the future.
Notable solutions
Day 4: Giant Squid [link]
I had already been stung a couple of times by programs that took several minutes just to parse in the input, so I had the idea that I could leave the input somewhere high in memory that nothing else is going to overwrite, and then just grab the input data straight out of memory without having to parse it.
So for day 4 I did exactly that. I wrote a program called read.sl that read integers from stdin and wrote them into memory starting at address 0xc000, and wrote the number of integers into address 0xbfff. Then part1.sl looks in 0xbfff to see how many integers there are (with an assertion that this number is 2500, so that it can notice if they are overwritten), and then operates on the input in-place starting at 0xc000:
var input = 0xc000;
var inputlen = *(0xbfff);
assert(inputlen == 2500, "inputlen = %d\n", [inputlen]);It did work but I think it may have been more trouble than it was worth. It turned out that parsing the input for this day wasn't all that time-consuming, and it adds extra stress of trying to make sure you don't do anything that will silently overwrite your input data. It's a fun idea though, I'm glad I tried it out.
Day 5: Hydrothermal Venture [link]
This was the first day where my 64K words of memory presented a problem. You're operating on a grid of 1000x1000 points. A million points is too many points to fit in 64K addresses. Even if you only use 1 bit per point of the grid, that's 62500 points, leaving only 1500 addresses remaining, which isn't even enough for the kernel, let alone the program to solve the problem.
Ben suggested splitting the input up into a number of smaller subgrids, and then solving the smaller grids consecutively. This was a pretty neat solution, and it worked fine. The only caveat was that splitting the input up into smaller inputs was more complicated than the actual problem! But that's all good fun. And at least it fits in RAM. That's exactly the kind of challenge I was looking for when I started doing Advent of Code on SCAMP.
Simon subsequently emailed me a solution to part 1 that runs in a single pass over the input file by sorting the input lines by x coordinate, and only looking at a single x coordinate at a time and testing which lines overlap in the y axis at that point in x, which is pretty cool. I believe he is the 2nd person ever to have written a SCAMP program.
Day 13: Transparent Origami [link]
I used a hash table as a sparse 2d array of points in this problem. Initially I wanted to use sprintf("%d,%d", [&x,&y]) to format the keys for the hash table, but I found this was running out of memory much more quickly than expected. I then realised that since my "characters" are 16 bits wide, and the integers that I'm formatting into the string are also 16 bits wide, I may as well just write the integer directly into the string! As long as I don't need to handle 0, this works fine and every integer fits in a single character. It's a much more efficient way to generate hash keys, because there's no time spent on formatting integers, and less memory wasted on storing characters. This is a good trick that I used a couple of other times as well.
I made sure that values of 0 don't prematurely terminate the string by adding 1 to every coordinate:
var k = malloc(3);
k[0] = x+1;
k[1] = y+1;
k[2] = 0;After completing day 13 I had a look at my sprintf() code and realised that it initialises the output string to 64 words long, growing it as required. This is too much in applications that format large numbers of short strings, so I've reduced the starting length from 64 to 8 words. But just sticking integers directly into the string is still better.
Day 17: Trick Shot [link]
After reading the problem statement I still didn't have a great intuition for what the trajectories looked like, so instead of writing a program to find the answer, I first wrote a program that would let me input candidate velocities and see whether the probe ends up flying over the target, under the target, or hitting the target.
I discovered quite quickly that once the y velocities are high enough, there is only 1 x velocity that results in hitting the target, because of the "drag" effect: the x velocity needs to be reduced to 0 at a time where the x position is within the target range.
I manually explored the search space and found a convincing-sounding candidate velocity, submitted it, and it was the correct answer. So I didn't write a part 1 solution at all!
Day 19: Beacon Scanner [link]
This was quite a big problem for SCAMP and my solution took several hours to run even though it was quite well optimised and (I believe) asymptotically optimal. I used the trick from day 13 of generating hash keys by sticking integers directly into characters, but went one step further by writing the function to do this in assembly language as this function is arguably the "innermost loop" of my program.
Day 22: Reactor Robot [link]
On part 1 you're operating on a 101x101x101 cube: that's just over a million points, which is too big to fit in memory. I reused the day 5 idea of processing the input in smaller chunks. I used a bit-set to represent the cube, and processed it in 4 quarters consecutively, so I only need about 16K words of memory per quarter.
For part 2 even this isn't enough. The correct solution is to use coordinate compression to remove all x, y, and z values that are not present in the input data, then operate on the much smaller grid, and then multiply the number in each cell of the smaller grid by the number of "real" grid cells it represents.
I started working on this but ran out of time before I got it working.
Day 23: Amphipod [link]
I solved part 1 by hand in my text editor, without writing any code at all, which was fun.
I tried to do the same thing for part 2 but gave up and started writing a program to solve it, but I ran out of time before getting it to work. But I later learned that Owen solved part 2 by hand, so I have had a couple more attempts at this but still can't do it. I can't even find any way to get all the amphipods into their correct homes, let alone the shortest way! I read on the subreddit that there is a 40x difficulty range between the easiest and the hardest inputs, so maybe I just got unlucky. That's what I'll tell myself.
Problems still to solve
Day 15 part 2
This is a shortest-path search on a 500x500 grid. The grid is derived deterministically from the 100x100 grid that is used in part 1, so lots of people on the subreddit are talking about how they cut down their memory usage by not putting the full grid in memory, but I think this isn't enough. Yes, it is easy to derive the edge cost for a given edge without storing the full grid, but the queue for Dijkstra's algorithm is still going to be too big to fit in memory, and you still need 1 bit per vertex for the visited set so that you don't re-visit previous points.
My plan is to put my priority queue and my visited set on disk, and use most of RAM as an LRU cache of disk blocks. My filesystem only supports 65536 blocks, so everything after the 65536th block is invisible to the filesystem, but my CompactFlash card is much larger than this. In LBA mode, one 16-bit word sets the upper bits of the block number, and another sets the lower bits. I can copy and paste the block IO code from the kernel, but just set the upper bits to some nonzero value, and then I can treat the CompactFlash card as a random-access block device rather than having all the overhead of my filesystem.
So once the input file has been read into memory, I'm not using the kernel to do disk IO. The only thing I still need from the kernel is console output, which is also easy to implement directly in my program, and then I don't need the kernel at all! This gives me about 48 more blocks' worth of disk cache, at the cost of having to reset the CPU when the program is done, instead of using exit() to return to the shell.
I am concerned that this will be too slow, but it sounds really fun to work on. I hope to solidify the design on paper and then film a video of my implementation. I think I'd like to output a 2d progress visualisation to the console, showing which parts of the grid have already been explored by Dijkstra's algorithm.
Day 22 part 2
I expect that I just need to implement the compressed coordinates version of my part 1 solution (which I already started), and go to some effort to minimise the number of bigint operations.
Day 23 part 2
I think the way to go here is to come up with a sensible representation of the map and then solve it with Dijkstra's algorithm. I started doing this, but my representation of the map was too convoluted. There are actually only 7 places that the amphipods can walk to other than their final destinations, so treating it as a generic grid that they can freely walk around over-complicates it quite badly.
Probably I want each of my nodes in the search space to represent the 7 locations the amphipods can park in, and a stack for each of the "rooms" that they end up in, and I'll want a function to calculate the path cost between a pair of points.
Day 24
I tried to solve this by reverse-engineering the input and working out what to do to make z == 0, but only managed to convince myself that it is impossible unless I can input a single digit with value 15.
I will probably have to read the subreddit carefully and try to pick the good ideas that other people have posted. Graham views the z register as a "stack" encoded in base 26, which is either pushed to or popped from depending on the value of each digit.
This makes sense, and I think the problem with my attempt at solving it by hand is that I greedily popped at every stage I could, whereas you actually sometimes need to push even if you can pop, just to ensure that you'll be able to do enough pops later on.
If you like my blog, please consider subscribing to the RSS feed or the mailing list: