Measuring motorcycle lean angle with a single accelerometer

The naive method of measuring motorcycle lean angle with accelerometers is to put a 2-axis accelerometer on the bike and measure the angle between the x acceleration and the y acceleration. This only works at a standstill. When the bike is moving, the measured angle would be 0. The purpose of the lean angle is to position the resultant acceleration vector so that it points from the centre of mass to the contact patch of the tyres, otherwise you will fall over. So how can we measure the lean angle?

A motorcycle that's leaning but not cornering looks like this:

The weight of the bike and rider unit is not positioned above the contact patch of the tyres, so the centre of mass is going to accelerate downwards and the bike will crash. (Alternatively, the weight and the reaction force from the ground are not aligned, leaving a resultant torque, so the bike is going to rotate and crash.)

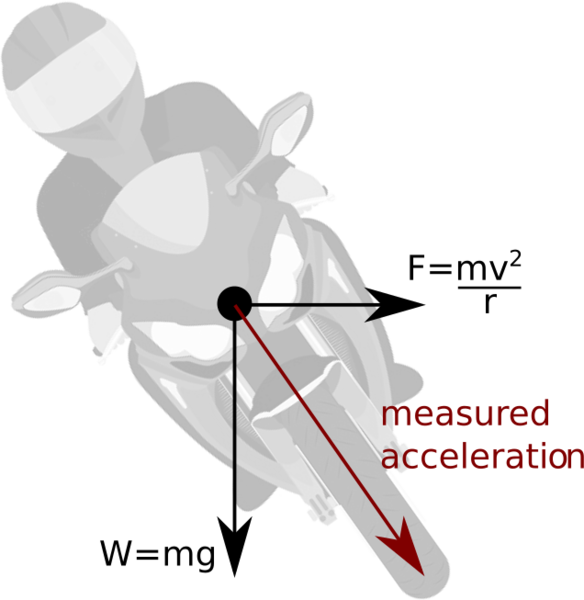
When cornering, we have the centrifugal force counter-acting the lean angle (or, if you prefer, we lean in order to counteract the centrifugal force):

(Reaction arrows omitted for brevity).

A 1-axis accelerometer measuring vertically in the bike's frame of reference would see acceleration corresponding to the red arrow.

Plotting this as a triangle (and turning the forces into accelerations) we get:

(v²/r unknown, g assumed constant).

Which we can solve with trigonometry to find the angle:

cos(θ) = g/a
θ = acos(g/a)

In reality this would not work quite so well (even if our accelerometer were perfect, there's no vibration, etc.) because:

1. We assume the forces are balanced. In steady state (constant speed, constant radius) this is true, but you need to temporarily unbalance the forces to make the bike lean. We would under-estimate lean when the bike is tipping into a corner and over-estimate when it is standing back up.
2. We assume a flat road. If the bike is under acceleration in the vertical axis (e.g. cresting a hill) then the effective value of g for the purposes of our triangle is incorrect. We would over-estimate lean in troughs and under-estimate on crests.