2025-04-30

Last modified: 2025-04-30 21:03:02

• Q factor
• Asymmetric resting torque

Q factor

John points out that the amplitude in my simulation grows forever because it doesn't use Q factor. So how is Q factor meant to work and how could I include it in my simulation?

Firstly I could have a checkbox to disconnect the escapement so that I could measure the pendulum on its own.

This is actually a great test:

This is showing some torque on the pendulum even with the escapement disconnected!

So I obviously have not correctly cancelled out the torque from gravity.

One good thing is it looks to be pretty symmetrical, and the magnitude is very low compared to the magnitude with the escapement connected, here's both on the same plot:

So that means the asymmetry in the frictional rest is probably not caused by calculating the gravity torque wrong, because the error in my calculation of gravity torque is too small to explain it. And perhaps the error in calculation of gravity torque is small enough to ignore.

So, on to Q factor. https://en.wikipedia.org/wiki/Q_factor

It is defined as the ratio of the initial energy stored in the resonator to the energy lost in one radian of the cycle of oscillation.

So I can look at how many radians the pendulum moved in the last timestep, work out what the torque loss to Q factor should be, and add that as a torque in Planck.js, and knock it off my calculation for the plot?

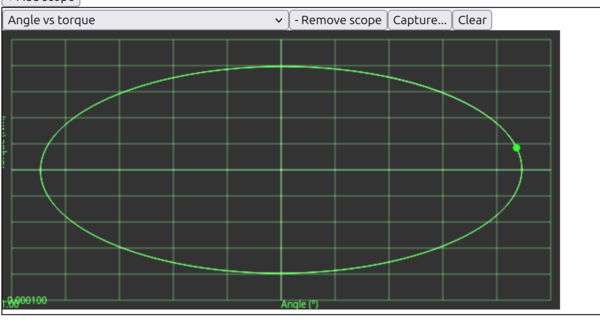
With Q factor set to 100 we see clear concentric circles, and the dot is moving around anti-clockwise:

And then do I need to add this, subtract this, or ignore it, from my total torque calculation for the plot?

I need to subtract it, and now the angle/torque plot with a connected escapement looks correct again.

The plot with a disconnected escapement is back to doing clockwise circles, the size of the circle being the amount of error in my gravity torque calculation.

Asymmetric resting torque

Oh! This may be because the resting surfaces are different distances from the pivot.

So it actually is true that the linear distance that the tooth scrapes across each surface is not the same. Could that be enough to explain it?