A few weeks ago I came up with an idea for a simple encryption device, then found that it had already been invented by Sir Charles Wheatstone around the 1860s. I ended up designing and 3d printing a replica of Wheatstone's cryptograph.
The principle
My idea was to have 2 wheels geared together, one with 26 teeth and one with 27 teeth. Each tooth would be labelled with a letter of the alphabet (with an extra character on the 27-tooth gear). The letters on the 26-tooth gear would correspond to the plaintext, and the letters on the 27-tooth gear would correspond to the ciphertext. A message is encoded by rotating the plaintext wheel clockwise until the desired letter is reached, and then writing down the letter displayed on the ciphertext wheel. One complete turn of the 26-tooth plaintext wheel results in 1 tooth less than one complete turn of the 27-tooth ciphertext wheel, which means the ciphertext alphabet gets shifted along by one place for every rotation of the wheel.
My first attempt was simply 2 gears with letters directly on the teeth:
To encrypt a message, you simply turn the left gear until the arrow points at your letter, and then write down the letter indicated on the right gear. Decryption is the same, but with the gears swapped. In order to select a different key, you would obviously need to print a gear with different labels on it.
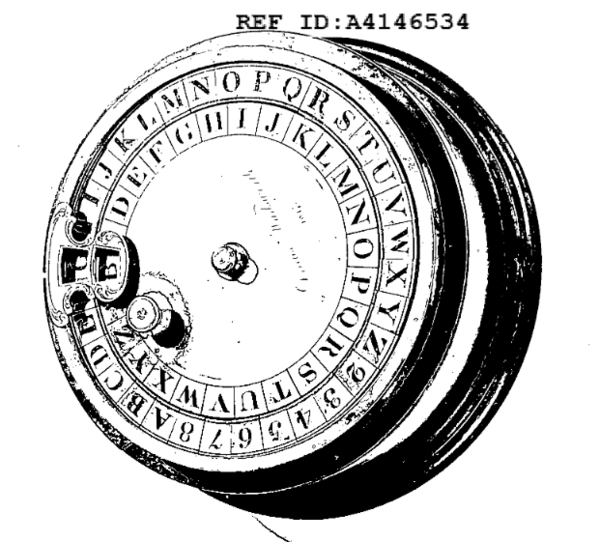
Wheatstone's device
It occurred to me that perhaps I'm not the first person to come up with this idea, so I searched online for various combinations of words like "26 tooth 27 tooth cipher" and came across Jerry Proc's page on the Wheatstone cryptograph, featuring this device:
(more photos and description on Jerry's page).
Wheatstone connected the 26-tooth gear to the ciphertext hand, and the 27-tooth gear to the plaintext hand. By the pigeonhole principle, it is not possible to unambiguously encode every possible letter from the plaintext disc (27 possibilities map to 26 possibilities). This is solved by putting a letter "Q" or "X" in between doubled letters so that at any given state there are only 26 possible plaintext characters ("HELLO" becomes "HELXLO").
The outer ring of letters is fixed in place, while the inner ring is a piece of cardboard, designed to have a scrambled alphabet written in pencil. (I understand that the original device had 26 removable letters that slot into holes, but they are easily lost over time and have been replaced with the cardboard ring).
The large hand is fixed to the shaft that it rotates on, while the small hand is only loosely clamped to its shaft by spring tension (provided by the large slit in it). The small hand can therefore be rotated independently of the large hand in order to synchronise the two hands.
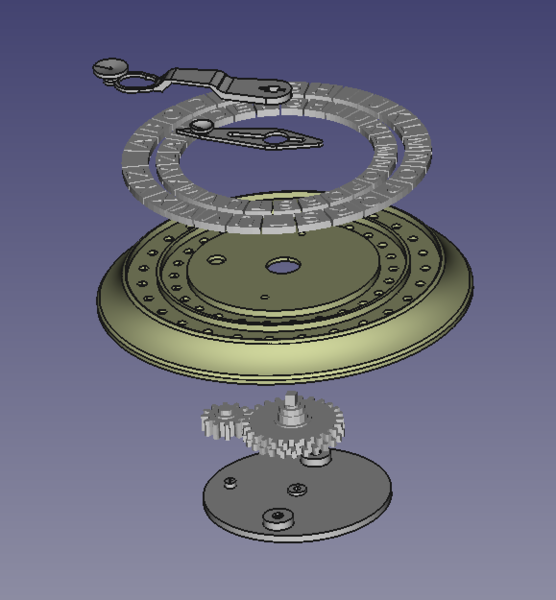
Inside, there are 3 gears:
This is a surprising arrangement and at first glance I was surprised that it could even work. It is actually impossible to design gears that have a different number of teeth, mesh perfectly against a common pinion, and rotate around the same centre. The tooth profile on the pinion dictates the tooth profile on the other 2 gears, and for a given tooth profile, changing the tooth count will change the diameter of the gear, which means the centre of rotation needs to move slightly in order to keep the gears meshing correctly. However, 26 and 27 are close enough tooth counts that it can be made to work plenty well enough. Quite clever really. Each gear has a shaft that sticks up through the top of the device, concentrically, for the hands to attach to, just like on a clock.
Interestingly, a similar device was actually invented about 50 years earlier, by Decius Wadsworth. I couldn't find any good photographs of Wadsworth's device, but there is this:
from a 1949 NSA document (mirrored), released to the public in 2014.
Cryptanalysis
I ended up exchanging some emails with Ralph Simpson, the owner of the Wheatstone cryptograph pictured above and on Jerry's page. Ralph directed me to some good resources on breaking the Wheatstone cryptograph:
- Macmillan's Magazine, 1871 (starting on page 335) (mirrored) (99 MB)
- The Friedman Lectures on Cryptology (starting on page 139) (mirrored) (11 MB)
- Several Machine Ciphers and Methods for their Solution (section II) (mirrored) (42 MB)
The latter being the most detailed.
To have a go at cracking it myself, I wrote a program to select a random copyright notice from /usr/share/doc, encrypt it with a random key, and then print out the ciphertext. I was able to crack all 4 that I tried, but only because I knew what some of the plaintext of a copyright notice looks like. I then tried selecting random files that aren't copyright notices, from /usr/share/doc, but I haven't yet been able to crack the only one I've tried.
There are a few observations that help in breaking the Wheatstone cryptograph:
The state of the device resets to the starting state after 26 revolutions of the large hand. If characters are selected from the plaintext wheel uniformly at random, we can expect to complete 1 revolution of the large hand every other letter, which means we can expect the device state to reset after 52 letters. Friedman notes that in practice this is closer to 50 letters due to non-uniform letter distribution.
If we see a doubled letter in the ciphertext (e.g. TT) then we know that this corresponds to 2 letters in the plaintext that are adjacent in the alphabet, but in reverse order (e.g. ED). This is because moving from E to D means turning the large hand through 26 steps, which is a complete revolution of the small hand, leaving it on the same letter it started on.
If we see a doubled letter in the ciphertext with another letter in between (e.g. TLT) then we know that in this case as well, the two T's correspond to adjacent-but-reverse-order letters on the plaintext disc (e.g. TLT could be EAD). Where the same letter appears in the ciphertext with n letters in between (e.g. TLFXT, n = 3) then we know that the repeated letter corresponds to letters in the plaintext that are in reverse order, with a maximum of n-1 other letters between them (e.g. TLFXT could not be HOARD because H and D are too far apart, but it could be STAIR because S and R are close and in reverse order).
It would be more secure if the plaintext disc were scrambled in addition to the ciphertext disc, as this would not allow the attacker to immediately start placing derived key characters in the right places relative to each other. It doesn't completely save the cipher, however, as Friedman has a method for cracking it regardless (although I don't fully understand it). Wadsworth actually figured this out despite having invented his device 50 years earlier, and on Wadsworth's device it was possible to scramble both discs.
If the cryptograph were modified such that the plaintext disc were scrambled and the ciphertext disc were in alphabetical order (or, more generally, if the plaintext disc is scrambled and the ciphertext disc is merely known to the attacker) then the cipher is very weak indeed. An attacker who knows the contents of the ciphertext disc has all the information he needs to recreate the movements of both hands. He can label his plaintext disc arbitrarily, and decrypt the message as usual. The resulting "plaintext" thus derived only differs from the real plaintext by the labelling of the plaintext characters, and is therefore solved as a simple substitution cipher.
3d printed replica
I spent some time modelling a 3d-printable replica of Wheatstone's device, mostly in FreeCAD but the gears and letters were done in OpenSCAD:
If you want to print your own, you can download the STL files: Download STL files (2.7 MB).
You'll want 2 small self-tapping screws to hold the gear cover on. And if you want the letters to be retained magnetically (and you do, because they're very small, light, and easily lost) then you'll want 106 tiny disc magnets. I used 2mm x 0.5mm, but up to 2.5mm x 1mm would work. Make sure you glue them all with the magnetic poles in the same orientation so that they don't repel the letters away. You also might consider printing the letters a couple of percent under-size if you intend to paint them.
Some of the details on Wheatstone's device are very small. I tried to print the gears at the original scale, but my 3d printer just can't make accurate teeth at the required precision, so I doubled the size of the gears. There is also a very fine thread on the top of the large-hand shaft, on to which a decorative nut is threaded to keep the large hand in place. Even on my over-sized imitation, the top of the shaft is only 3mm wide. There was no way I was going to be able to print a thread this small so I didn't even try, I just made the hand a tight push-fit on to the square end of the shaft.
The strange-looking bend in the large hand is just there to allow the small hand to pass underneath.
I put a tiny magnet in the bottom of each letter, and a tiny magnet in the base in the place of each letter, so that the letters remain in place even when held upside down, but can easily be removed and reordered.
I spent quite a long time priming and sanding the top surfaces of the cryptograph so that it looks nice and smooth when painted.
The gear cover has that fun hexagon pattern so that you can look in the bottom and watch the gears moving. This is accomplished by slicing a solid part for 3d printing with 0 top layers and 0 bottom layers, so that the infill pattern is visible. It can't be used for all parts, but where it can it's a nice effect. I didn't bother priming and sanding the bottom surface, but it looks pretty bad where it didn't stick to the print bed properly, so perhaps I should have:
The letter tiles are painted white, with a permanent marker rubbed over the raised parts to make the letters black.