How to win at Scotland Yard
Thu 4 April 2019Tagged: ai
I've been playing Scotland Yard recently. It's a board game in which one player plays as "Mr. X", and the other players are all detectives, played on a map of London. Mr. X moves in secret, and his goal is to evade capture for 24 turns, while the detectives' goal is to capture him before 24 turns are up. It's a brilliant game.
I wrote a Perl implementation of the game, including a basic AI to play as both Mr. X and the detectives.
Paul P. on boardgamegeek has written a strategy guide for Scotland Yard from experience and first principles, which is quite helpful. This post is about a more data-driven approach, from tens of thousands of simulated games, to gather more information about the game.
Paul P. says Mr. X is likely to win ~30% of the time. I'd agree with this. That means if you're playing as Mr. X, and you lose, it's not necessarily your fault. If you can win as Mr. X more than 30% of the time, you're doing well. In the simulations, Mr. X won on average ~17% of the time, but with the use of 2X cards he would have done better.
Throughout this post we'll talk about win probabilities: these are always from Mr. X's perspective. If the win probability of a certain configuration is 20%, that means Mr. X is 20% likely to win, which means the detectives are 80% likely to win.
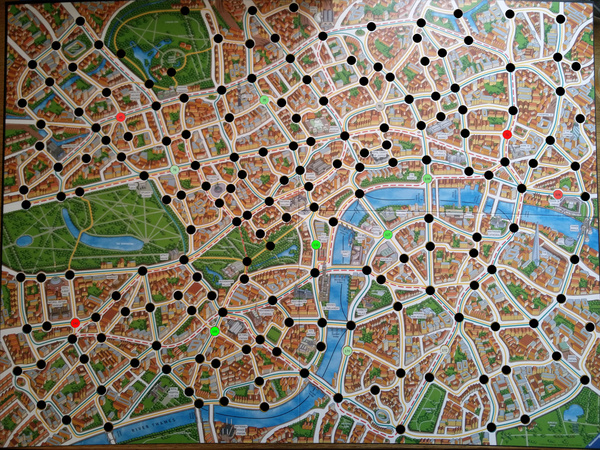
1. Mr. X's starting station is critical
Mr. X's winning chances from each starting station. The mean (grey) is 17%. Green is better, red is worse.
The single most significant factor that I could find to determine how likely Mr. X is to win, from a dataset of 64k games, is the station he starts on. From the worst starting station (146), Mr. X won only 6% of games. From the best starting station (166), he won 27%.
| Starting station | Winning chances |
|---|---|
| 166 | 26.9% |
| 132 | 25.6% |
| 127 | 22.8% |
| 104 | 20.8% |
| 35 | 20.7% |
| 170 | 19.0% |
| 78 | 18.6% |
| 172 | 17.3% |
| 51 | 16.8% |
| 106 | 10.5% |
| 45 | 8.7% |
| 71 | 7.3% |
| 146 | 6.2% |
There are 13 possible starting stations, and Mr. X is supposed to shuffle them and draw one at random.
It's unfortunate that the starting station is selected at random, given that it is so critical. I therefore propose a slight rule change:
Before the detectives draw their stations at random, Mr. X is allowed to choose his starting station freely from the set of Mr. X starting stations, instead of having to pick one at random.
You might think "but Mr. X will always pick station 166, and the detectives will know that, so it won't work any more", but I tried a variant of the game where Mr. X always starts on station 166, and his winning probability was only reduced from 27% to 26%, so if I were playing as Mr. X I would almost always choose to start on station 166 or 132: even if the detectives know you've done this, you're still much better off than choosing at random.
If you want to cheat, and you think you'll get away with it, you should start on station 181. This is not among the set of allowable Mr. X starting stations in the official game, but from station 181, in my simulations where Mr. X is allowed to start on any station, Mr. X won 44% of games compared to the 27% of station 166. (But note that there were only about 200 simulated games for each of the 115 possible starting stations that are at least 2 hops away from the nearest detective starting station, so this number probably has quite large error bounds).
I also tried to generate an alternative set of 13 starting stations which would provide more balance, but I couldn't find 13 stations spread all across the board from which Mr. X had reasonably similar chances of winning:
Mr. X's winning chances from a wider set of possible starting stations.
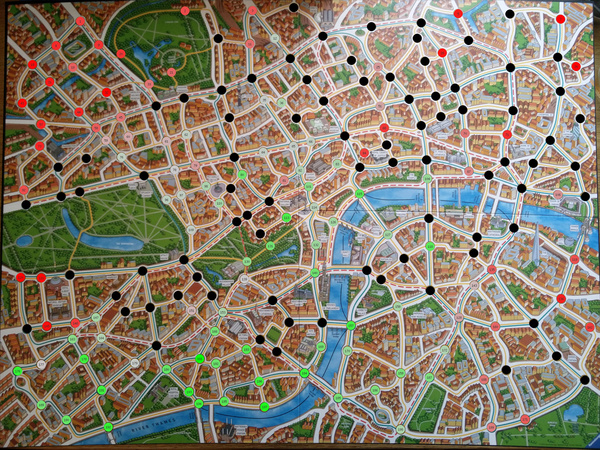
2. Some areas of the board are much worse for Mr. X than others
Mr. X's winning chances from each visited station. The median (grey) is 35%. Green is better, red is worse.
Mr. X won 80% (!) of simulated games in which he managed to step on station 79 (the best station). He won only 11% of games in which he stepped on station 7.
(It should be noted that Mr. X only managed to visit station 79 in less than 1% of games, whereas he was forced onto station 7 in 10% of games.)
It doesn't quite follow that you should always head towards station 79, because your real goal is to evade capture, not to visit station 79. But if you can step on station 79, and there isn't currently a detective on an adjacent station, you probably have good chances of winning.
I tried feeding this data back into the AI to see if it would play any better. I modified the evaluation function to multiply the evaluation of each position by the prior win probability of the station that Mr. X is on.
| Detectives | |||
| With data | Without data | ||
| Mr. X | With data | 15.6% | 17.6% |
| Without data | 21.0% | 16.7% | |
So it doesn't change his chances of winning by a lot. Surprisingly, Mr. X's best chance of winning is when he is ignoring the "good" stations, and the detectives are going out of their way to stop him from visiting them!
I'm not sure why the difference in winning chances is so small, when the observed difference in winning chances between different stations is so high. Probably because the locations of the detectives constrains Mr. X's movements so much that he has a lot of difficulty actually aiming for the high-value stations.
The heatmap of winning chances probably serves best as a predictor of who is going to win, rather than as a guide of where to move to. That is, if Mr. X is on a station coloured bright green, he has a good chance of winning. But Mr. X has to primarily evade capture, and only occasionally has the freedom to deliberately move towards the bright green areas.
3. Where the detectives should move in the first 2 turns
In the first 2 turns, the detectives have no information about Mr. X's location, other than that he started at one of the possible starting stations. On turn 3, Mr. X has to reveal himself. From the allowable starting stations, Mr. X can reach any station except: 2,5,18,19,121,150,162,175,182. (That is, every station except those is within 3 hops of at least one of the allowable Mr. X starting stations).
So the goal of the detectives is to spend the first 2 turns to move to well-connected stations, to minimise the maximum possible number of hops between the detectives and Mr. X. This distance is minimised by moving as follows:
| Starting station | Head towards any of | Max. hops to Mr. X |
|---|---|---|
| 13 | 51,55,65,66,68,71,79,82,84,88,102,105,111,128,140 | 6 |
| 26 | 51,52 | 6 |
| 29,91,117 | 89 | 5 |
| 34 | 13,23,65,79 | 6 |
| 50 | 23,51,66 | 6 |
| 53 | 52,55,68 | 6 |
| 94 | 46,79 | 6 |
| 103,112 | 67 | 5 |
| 123,138 | 111,153 | 6 |
| 141 | 128,140 | 6 |
| 155 | 139,140,153 | 6 |
| 174 | 128 | 6 |
In cases where the starting station has a single-hop connection to the designated destination, you shouldn't use it! You should ensure that you take exactly 2 turns to move to the designated station, so that you're well-positioned when Mr. X reveals himself on his 3rd turn.
In cases where two or more detectives have the same designated station (for example, 29, 91, and 117 all want to go to station 89), obviously only one can actually go there. The detectives will have to discuss amongst themselves to find the best allocation of detectives and stations.
4. Playing a turn as Mr. X
First, look at the set of possible moves you have. For each possible station, count the number of hops to the nearest detective. Note that the nearest detective may be quite far away if the station has bus or train connections. If a candidate station is only 1 hop from a detective then you probably shouldn't move there, because there is a risk that the detective will step on you next turn.
If you now have more than one candidate station that is more than 2 hops from the nearest detective, consult the heat map of winning chances to decide which one is best, and try to move to greener stations rather than redder ones.
If you have exactly one candidate station that is more than 2 hops from the nearest detective, you should probably play that one. But note that if the detectives already know where you are, they'll also know that you are likely to move to this station, so you may have better luck sneaking past a detective in the opposite direction if a.) you are reasonably confident that they know you only have one candidate station more than 2 hops from them, and b.) moving to that candidate station while the detectives know where you are would result in them "closing the net" over the next few turns.
If you have no candidate stations, then you're in trouble. It's probably time to spend a 2X card if you have one. If you have one, do the same procedure again, but look 2 hops ahead instead of just 1. You're looking for candidate stations that are at least 2 hops from the nearest detective. Remember that in 2 hops you can move back to the station you started on.
If you have no candidate stations and no 2X cards, then you have to try to work out what the detectives will do next turn, and move to a station that you think they will not move to.
Finally, if you're on a station that has bus, train, or ferry connections, consider using a black ticket so that the detectives won't know how you travelled, particularly if the detectives know which station you are on. You should never use a bus or train ticket unless doing so does not reveal extra information about your location (for example, because you're about to reveal your location anyway, or because your only legal move is a bus or train journey).
5. Playing a turn as the detectives
In the first 2 turns, you should move towards the well-connected stations as detailed in the table above.
Once Mr. X has revealed himself on turn 3, you should start keeping track of the set of possible stations that he could be on. There's no reason not to do this on a sheet of paper. After Mr. X has moved, write down the set of possible stations he could be on. This is the set of all stations that are reachable, via the ticket he used, from any of the stations he could have been on last turn. After the detectives have moved, you can cross off all of the stations that the detectives moved to, because the game would have ended if Mr. X were there.
(If the set of possible stations gets too large to follow, then you've effectively lost him: you should revert to the strategy of moving to well-connected stations to try to close in again after he next reveals himself).
Think about all of the detective moves before moving any of the detectives. Sometimes you have 2 detectives that can cover the same station, and it is important to decide which one to send there based on which station you want the other one to cover.
AI limitations
The AI in my Perl implementation is a minimax search with iterative deepening, and a time limit of 30 seconds per turn.
30 seconds per turn is too long to do tens of thousands of games, so for the simulations I limited the search depth to only 1 ply: on each turn, it considers all of the possible moves, evaluates the position, and then plays the move that is best, without any recursive searching of the opponent's responses.
The evaluation function is as follows:
- compute the shortest path from Mr. X to each detective
- compute the number of possible stations that the detectives know Mr. X could be on
- the score for Mr. X is the length of the shortest path to the nearest detective, plus 1/100th of the sum of the shortest paths to each detective, plus 1/100th of the number of possible stations
Notably, this does not include any value for black tickets, which means Mr. X will always play a black ticket if it expands the set of possible stations he could be on, regardless of whether that is actually a good use of the black ticket. It also does not include any value for 2X tickets, but this is "fine" because the AI doesn't know how to use 2X tickets.
Since it's a zero-sum game, the detectives use exactly the same evaluation function as Mr. X does, but they have to evaluate it for each possible station Mr. X could be on and assume the worst. The detectives team always had 4 detectives. When Mr. X is playing against 5 detectives he presumably has a harder time of it.
The biggest weaknesses of the AI used for the simulations are the lack of 2X tickets, and the limited search depth.
Open questions
- How significantly does the introduction of a 5th detective affect Mr. X's chances? Would giving Mr. X a 3rd 2X card keep the game more balanced with 5 detectives?
- Assuming the detectives move according to the prescribed table, what are the optimal opening moves for Mr. X, from each possible Mr. X starting station, to maximise the minimum distance to the nearest detective upon revealing Mr. X on turn 3? (For 4 detectives, there are "16 choose 4" possible detective starting configurations, multiplied by 13 possible Mr. X starting stations, = 23660 possible combinations, which is large but brute-forceable)
- Is it better for Mr. X to maximise the number of possible stations he could be on, or the number of hops to the nearest detective?
If you like my blog, please consider subscribing to the RSS feed or the mailing list: