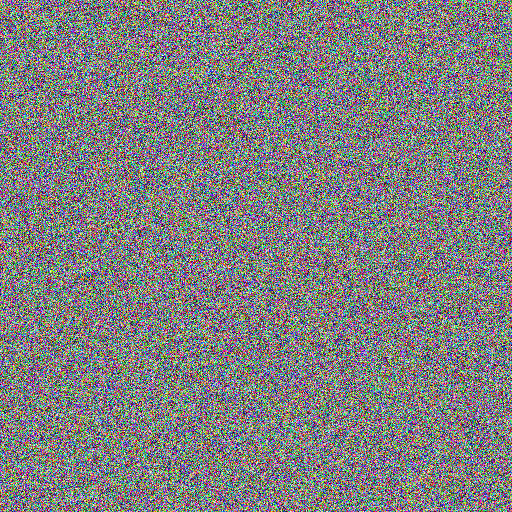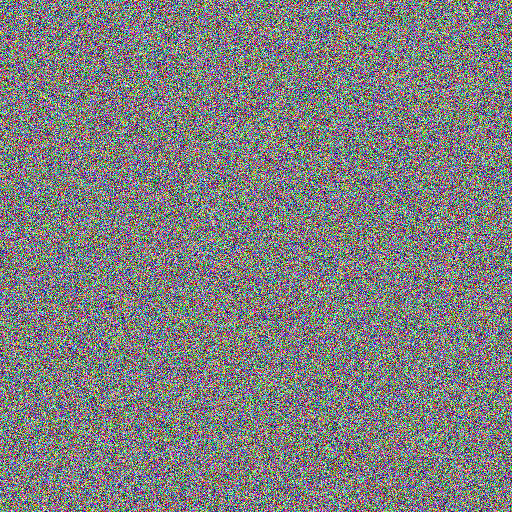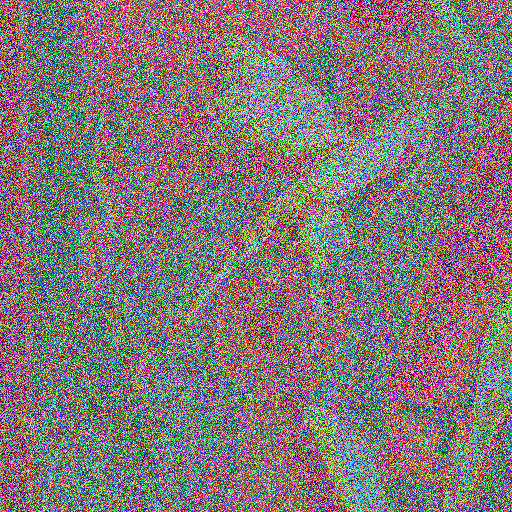A visual demonstration of the perils of key reuse in a one-time pad

Sat 17 February 2018
Tagged: cryptography

I was playing with applying one-time pad encryption to images recently, and stumbled across some interesting visualisations that I want to share.

One-time pads

From Wikipedia:

In cryptography, the one-time pad (OTP) is an encryption technique that cannot be cracked, but requires the use of a one-time pre-shared key the same size as, or longer than, the message being sent. In this technique, a plaintext is paired with a random secret key (also referred to as a one-time pad). Then, each bit or character of the plaintext is encrypted by combining it with the corresponding bit or character from the pad using modular addition. If the key is truly random, is at least as long as the plaintext, is never reused in whole or in part, and is kept completely secret, then the resulting ciphertext will be impossible to decrypt or break.

The operation that combines the plaintext with the key doesn't actually have to be modular addition, in fact I believe it can be any bijective function. XOR is often more convenient than modular addition as it means the decryption operation is the same as encryption.

If we have a message m made up of N elements, and a key k of at least N elements, an encryption operation ⊕, and its inverse ⊖, then we can produce a ciphertext c of N elements by:

c_i = m_i ⊕ k_i

and retrieve the message from the ciphertext by:

m_i = c_i ⊖ k_i

Simple enough.

One-time pad on images

An image is a 2-dimensional array of pixels, and a pixel is a 3-tuple of numbers representing brightness for red, green, and blue. It's therefore easy to see how we might apply one-time pad encryption to the pixel values of an image independently of the actual bytes stored in the file format that is used to represent the image. This is helpful as it allows us to see what is going on visually.

I wrote a Perl script to XOR 2 images together.

So here's a picture of Lenna:

and here's a randomly-generated key image:

And we get Lenna XOR key =

Hopefully you agree that this looks pretty random. Hopefully you also agree that it is a different random image to the key. Taken alone, this image contains no information about Lenna at all. It is only by combining it with the key image that we can recover Lenna.

Key reuse

The reason keys mustn't be reused in a one-time pad is that it allows an attacker to learn some information about the underlying plaintexts.

If you encrypt messages m₁ and m₂ with the same key k, then you get:

c₁ = m₁ ⊕ k
c₂ = m₂ ⊕ k

Individually c₁ and c₂ are unbreakable, but an attacker who intercepts them both can simply compute:

c₁ ⊖ c₂
= (m₁ ⊕ k) ⊖ (m₂ ⊕ k)
= m₁ ⊖ m₂

And he's now derived a combination of the 2 plaintexts, with no key material mixed in whatsoever. If either of the plaintexts is known or easily guessed, the other becomes known immediately. But even in the absence of one or other known plaintext, there is usable information here.

Take this image of my face, for example:

After encrypting it with the same key image we used for Lenna above, we get jes XOR key =

Which looks OK.

But if our ciphertexts were intercepted, the attacker would be able to XOR the 2 images together and retrieve an image of Lenna XOR jes =

From which it's easy to identify both Lenna and jes! No bueno.

Weak key generation

I also tried generating a key image where all pixel values between 50 and 150 are fixed at 100, but is otherwise completely random:

And it looks pretty convincing. I personally can't spot anything obviously wrong with it.

But when we encrypt Lenna using this weak key, we get:

Which leaks enough of the plaintext information into the ciphertext that we can just about make out Lenna from just one intercepted ciphertext, and with no extra processing required.

A challenge

If you found this interesting and want some more fun, you might enjoy the following challenge...

Analysts at the Graphical Cryptography Head Quarters, along with their friends at the Notional Security Agency, have intercepted a series of images that were exchanged between suspected foreign spies. Baffled by the content of the images, they've called on you as their last hope. Can you crack the code, decipher the images, and save the world?

Download the images at /ipfs/QmPTvvKRGdHWH95imZemLSJYuJWdE1EewWDKjq2bPzjL6G.

If you solved it, or if you can't solve it and want to know the solution, or if you aren't interested in the challenge and just want to talk one-time pads, please email me: james@incoherency.co.uk.

If you like my blog, please consider subscribing to the RSS feed or the mailing list: