2025-04-05

Last modified: 2025-04-05 21:20:07

Targeted blends

I think I'm satisfied enough with the idea that Combinators jump on top of Modifiers when the tree needs rewriting. Just keep it to a minimum, only do it when there are targeted blends that require it.

And the method is something like:

Clone the tree, keeping uniqueId intact.

Label each node with the set of surface ids it can yield.

Nodes are either:

• combinator: more than one child & has "isCombinator" true or something: can yield any of the surface ids its children can yield
• modifier: has at least 1 child but is not a combinator: yields the surface id of its first child
• primitive: yields its own uniqueId as a surface id

Blends only apply at combinators. (For now: but eventually we will want an abstraction over "surfaces" so that LinearPattern etc. can give a different surface id to each surface of each copy).

Now iterate over combinators starting from the ones furthest from the root.

So then at each combinator, look at the set of surface ids you can get from the left child, and for each one look at the set of surface ids you can get from the right child.

Say left is (1,2,3) and right is (4,5).

Now look up the targeted blends for each of those ids, and see if the other surface of the targeted blend is on the other child of the combinator. If so, rewriting not needed here.

Then build up the set of all possible pairs of surface id.

{ (1,4), (1,5), (2,4), (2,5), (3,4), (3,5) }

Now look up blend parameters for each of these pairs. If so, rewriting not needed here.

(Also, if we eventually get a Link node then either Link ought to yield new surface ids, or else instead of checking that all of the blend arguments are contained as children, we need to check that none of the blend arguments are not contained as children. Because there will be duplicate ids in the tree.)

Now in the 2 places that we said "If so, rewriting not needed here"... If not, work out how to do the rewriting?

If the node does not contain all of its blend arguments, then the node needs to be moved up the tree. Without loss of generality, everything above a Combinator is also a Combinator.

So we transform like so:

C1(C2(a,b), c)

Where C1,C2 are combinators and A,B,C are arbitrary subtrees. Let's say we want a blend between A and C. So now C2 doesn't have all its blend arguments as children, so C2 needs to move up.

We rewrite to:

C2(C1(a, c), C1(b, c))

So if we had:

C1: parent=null, left=C2, right=c
C2: parent=C1, left=a, right=b

We now change to:

C1a: parent=C2, left=a, right=c
C1b: parent=C2, left=b, right=c
C2: parent=null, left=C1a, right=C1b

So if C2 is the left argument of C1, and we grab out C1's right argument X, then for our children A,B, we replace them with C1(A,X),C1(B,X) and then delete our parent and reparent ourselves to its parent.

So that's the method for rewriting to make sure the combinator contains all its blend arguments.

In the event that the immediate parent of C1 is not a combinator, we instead take the Modifier chain that sits between C1 and C2, and push it down to be on top of C2's children.

So:

C1(M(C2(a,b), c))

becomes:

C2(C1(M(a), c), C1(M(b), c))

And if that still doesn't get you all of the blend arguments as children, then move C2 up another level, etc.

And then once we have all the blend arguments as children, we have the issue if not all the blend parameters are the same.

Let's say we have:

C(a, b)

Where a,b are subtrees that can yield (1,2,3) and (4,5) as surface ids, and we only want a blend between 1 and 4.

For a subtree to be able to yield more than one id its root must be a Combinator (without loss of generality).

Actually I think this case would be solved automatically. Because for there to be a blend between 1 and 4, there must be a child that yields 1 and a child that yields 4. And earlier on when we reached the child that yields 1 we would have noticed that its blend argument 4 was not present, and rewrote the tree to fix it.

So... is that enough?

Probably I do test-driven development for this.

So we take in a tree of TreeNodes, and a set of blends, and give a rewritten version of the tree where every Combinator has the same blend parameters regardless of what comes out of its child nodes, and then compile the rewritten tree into our SDF.

Could the rewriting be done as part of the peptide() function? Not obviously straightforward.

I guess what I'm struggling with is the fact that peptide() seems to be defined for any TreeNode, without regard for the requirement that the Combinators have consistent blend params.

So maybe blendParams() throws an error if that is not satisfied? And then it's only safe to call peptide() on a rewritten tree.

Should peptide() take the array of children as an argument? And then we can change which children we give to which nodes without having to clone the nodes. No, because those children in turn will have children.

Maybe cloning the tree is not a problem.

And what do we call the operation of rewriting the tree to make blends work?

Another issue is that my Combinators can have more than 2 children. So I think first the Combinators need rewriting into a form that only has 2 children.

I wonder if instead of rewriting the complete tree, we instead have some intermediate step between the TreeNode and the peptide() call, that returns a "good" tree.

Like a normalised() or something, that by construction returns a tree where all the Combinators have static blend parameters.

To start with just make normalised() break up Combinators so they always have 2 children.

Then maybe rewrite the complete "normalised" tree afterwards.

OK, we'll turn the "normalised" tree into a simpler tree representation that just has:

• combinator: 2 children
• modifier chain: 1 child
• primitive: 0 children

and each node has a reference to the original TreeNode(s).

Tests:

• does normalised() work?
• does possibleSurfaceIds() work?
• does fromTreeNode() work?

Adding a test for normalised(), it should turn:

Union(Subtraction(Sphere,Sphere,Box),
      Intersection(Sphere,Box,Gyroid),
      Union(Sphere,Box,Box))

into:

Union(Union(Intersection(Intersection(Sphere, Negate(Sphere)), Negate(Box)),
            Intersection(Intersection(Sphere, Box), Gyroid)),
            Union(Union(Sphere, Box), Box))

So 19 nodes in total. But I'm only seeing 12. The first discrepancy is that Subtraction(Sphere,Sphere,Box) has only turned into Intersection(Sphere, Negate(Sphere)), i.e. it's no longer subtracting the Box.

In fact all of them only get the first 2 arguments instead of all 3, apart from the top-level Union which seems to be working correctly.

So normalised() is not working properly.

It was because constructing a new node with some given children also deletes those children from their previous parent! So do it by iterating over a copy of this.children instead.

And normalised() also is not preserving possibleSurfaceIds() values.

Oh, lol, I had 2 implementations of clone() - one that rewrote uniqueId and one that did not, I renamed the latter now.

So normalised() and possibleSurfaceIds() are looking good now.

Next up is whether TreeRewriter.fromTreeNode() is making correct-looking intermediate trees?

So, make some complicated tree structure, call fromTreeNode() on it, and check that it is going through cloneWithSameIds() and normalised(), and that modifier chains are collapsing into single nodes, and that the uniqueId of the leaf nodes is unchanged.

Then we get on to actually rewriting the tree.

OK, fromTreeNode() looks good. Let's actually make sure toTreeNode() can correctly reconstruct a tree.

Good, working now.

So to test rewriting a tree, the basic case is if we don't ask for any blends, you have to produce a tree that is equivalent to the input tree.

And then if we want multiple blends but they are already satisfied by the input tree, make it still equivalent.

And then if we ask for a single blend that requires a simple rewrite, with no modifier chains, and only one level of applying distributivity, it should handle that.

And then do a big complicated test.

The trivial cases are obviously passing without having to implement rewriteTree(). So now on to the "simple blend" case.

We have:

Union(Intersection(Sphere, Gyroid), Box)

with a blend between Sphere and Box, so we need to rewrite to:

Intersection(Union(Sphere, Box), Union(Gyroid, Box))

Currently it is not quite working because when we duplicate Box in the tree we can't set its parent pointer.

So steps are:

• work out what to do about parent pointers when duplicating node references
• distribute over right child as well as left child
• provide satisfiedBlends() to decide whether the node is good or not
• add more tests

In toTreeNode() I can just cloneWithSameIds() every TreeNode to make sure "duplicates" are all unique.

And for passing around blends, I needed to make normalised() pass on the blends field, otherwise when the Document gets normalised it no longer has the blends. And now the simple tests are working.

So the next thing is "looking through" modifier chains. We could either do this by making the distributivity code handle it, or by attaching the modifier chain as a property rather than a node of its own.

The starting point is that Modifier(Combinator(a, b)) is equivalent to Combinator(Modifier(a), Modifier(b)).

So I think just before we check if our child Combinator node is happy with its blends and rewrite it if not, we should see if our child is a Modifier node, and if so see if its child Combinator node is happy with its blends, and if not rewrite it.

Rewriting the tree by looking for blends that are not satisfied is not quite the right thing to do. Because after:

Union(Intersection(Sphere, Gyroid), Box)
->
Intersection(Union(Sphere, Box), Union(Gyroid, Box))

With a blend between Sphere and Box, we now think the second "Union" node is no good, because "Box" is meant to have a blend and that node can't do it.

We can satisfy a blend if the only ids that come into us are blend arguments. If we see both ids coming from the same child then we know the blend is handled deeper. If we only see one of the ids then we know the blend will be handled higher up.

The problem is if we see one id coming out of one child and the other id not coming out of the same child, but more than 1 possible id from one child or the other. Then we know we are responsible for the blend but we can't fulfill it.

No, not right. Look at the example above. After the rewrite, the Intersection's right child can generate Gyroid and Box, but still isn't responsible for the blend between Sphere and Box, because the left child handles Sphere and Box.

So as long as one child is seeing both ids, we don't care what ids we see from the other child.

Whoa! It might be working, even with modifier chains. Passing tests, at least.

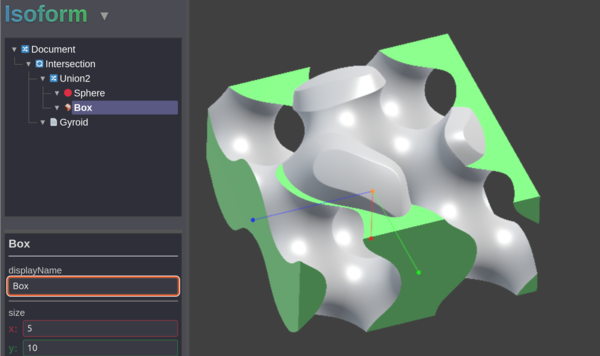
I'm going to make the actual program render a model of:

Intersection(Union(Sphere,Box), Gyroid)

In which (Sphere,Gyroid) has a blend, and see what it looks like.

Yes!!! It is working.

And no needing to fade out the blend as it approaches the box.

Ah... there are some discontinuities in the field though.

Oh, but this I'm still trying to set blend radii with a runtime lookup. I need to make the tree rewriting code set the blend params on the appropriate TreeNodes.

Now I am trying to apply the blend parameters to the rewritten tree, but it doesn't appear to be working. When I log the tree to the console I see the parameters I expect, but the rendered image seems to ignore them.

There's also the issue that we get different uniqueIds for some nodes in the rewritten tree, which leads to shader source not matching, which leads to spurious recompiles. But fix that later.

OK! The issue with blend parameters not getting applied is something to do with setting uniforms. If I make it use P.const() instead then it works!

Check it out:

There is a chamfer between Sphere and Gyroid but not Box!

And no fading out near the Box, and no discontinuous field near the Box. Great success!

OK, found a bug. If I delete the Sphere and replace it with a new one, then it is no longer intersected with the Gyroid:

Also for some reason the shader takes a very long time to compile with that sphere added.

So, todo is:

• fix whatever is the issue where the Sphere doesn't intersect with the Gyroid (add a test; it could be as simple as it messes up if you ask for a blend where one of the arguments doesn't exist)
• make it work with this.uniform() instead of P.const(), also maybe instead of using this.blendRadius or whatever, the uniform should refer to the parameter of the blend
• recompiling the shader every time
• more complex unit tests
• particularly make sure we combine multiple things into one even if there is more than one id, as long as all combinations of id take the same blend parameters
• UI for applying blends