2024-11-16

Last modified: 2024-11-16 23:37:13

Clock

I have the new escape wheel fitted now, I also adjusted the spring mounting so I think the spring is no longer rubbing the balance shaft.

But it still doesn't work. It loses too much energy with every oscillation. If I have less drive weight then it wastes less in friction but provides less impulse, and the opposite if I have more drive weight. I can't get it to sustain amplitudes large enough to actually reach frictional rest.

I have a tiny amount of end shake in the balance shaft, which is what I want. I have taken the weights off the balance wheel because I found that it swung freely for more oscillations that way, which suggests it is losing a lower percentage of its energy to friction each swing (?).

I tried with the weights added back. Doesn't help.

So the next things to try are a drop of oil in the bottom balance pivot, and fixing the pallet geometry so that we get more impulse per cycle.

Predictably, oiling the pivots didn't help. I also oiled the pallets and that didn't help. (Has oiling one of these models ever helped? Why do I persist in trying it?).

We can actually work out what proportion of energy is spent on impulse versus frictional rest.

Work = Force * Distance

We have three ways to lose energy from the escape wheel:

1. impulse
2. frictional rest
3. drop

To work out the energy spent on impulse, find the linear distance d_imp moved by the escape wheel during the impulse.

To work out the energy spent on frictional rest, you need to know the coefficient of friction mu, and the amplitude, and then look at the linear distance d_fric that the escape wheel tooth rubs on the back side of the pallet.

To work out the energy wasted on drop, find the linear distance d_drop moved by the escape wheel during the drop.

We'll say that for a given drive torque T and escape wheel radius r, we have F = T/r at the escape wheel tooth.

W_imp = F * d_imp
W_fric = F * mu * d_fric
W_drop = F * d_drop

From looking online it looks like about 0.5 is a good value for mu.

Looking in CAD, we have:

• escape wheel rotates about 1.7 deg. during drop.
• escape wheel rotates about 1.6 deg. during impulse.
• escape wheel diameter is 220 mm.
• frictional rest diameter is 14.8 mm.
• frictional rest only occurs at amplitudes amp beyond 160 deg..
• d_drop is 1.7/360 * 220 * pi = 3.26 mm.
• d_imp is 1.6/360 * 220 * pi = 3.07 mm
• d_fric is (amp - 160)/720 * 14.8 * pi.

To find out the amplitude if there were no other losses at all, we can set W_imp = W_fric, i.e. find out when the energy given in impulse is exactly cancelled out by the energy lost to friction, and solve for amp.

W_imp = W_fric
F * d_imp = F * mu * d_fric
d_imp = mu * d_fric
3.07 = 0.5 * d_fric
6.14 = d_fric
6.14 = (amp - 160)/720 * 14.8 * pi
6.14 = (amp/720 - 2/9) * 46.5
0.132 = amp/720 - 2/9
0.354 = amp/720
amp = 255

So for any given drive torque it should run at an amplitude of 255 deg. if there were no losses in the pivots. And if there are losses in the pivots then, contrary to my intuition, increasing the drive torque should always increase the amplitude, tending towards 255 degrees. I had previously thought that increasing the drive torque too far would mean it was slowing it down too much during frictional rest, but it turns out that the drive torque completely cancels out if you ignore losses in the pivots. If you add losses in the pivots then adding drive torque only helps to add amplitude.

I could try and add as much drive torque as I can manage now, and see if we can get anywhere near 255 degrees.

Doesn't really seem to help. I think the drop is too big and the energy from the drop is slowing it down. The calculations above only apply if the amplitude is large enough to enter frictional rest. If you don't enter frictional rest, then the impulse distance is reduced and you are getting your impulse from the drop instead? Maybe? So if the drop distance calculated above exceeds the impulse distance, then you are not getting enough energy from the impulse to be able to counteract the energy from the drop, so you can never have frictional rest in steady state.

So the obvious parameters to improve are:

• reduce friction (not a lot I can do)
• reduce drop
• increase escape wheel tooth distance during which impulse is delivered, preferably by robbing it from the drop
• decrease frictional rest diameter (makes depthing more sensitive)

So I think the plan is just to adjust the offset between the impulse faces to increase the ratio of impulse to drop.

If the drive torque is too high then the escape wheel bends during frictional rest and skips teeth.

I think progress is being made here. I will try to film a clip of it running later.

I think it's important to minimise the amount of recoil, because recoil is an energy threshold that the balance wheel needs to overcome in order to be able to enter frictional rest.

I wondered about putting an undercut on the impulse face. In fact, it is basically undercut already. So what I really mean is increase the offset between the faces, which is cnotrary to my previous idea that the faces wanted to be as close together as possible.

Actually, increasing the undercut increases the amount of recoil, I think. So you do want to minimise the undercut, with the condition that you need some space for the drop so that it actually works.

OK, I think stop messing about with the pallets. It's obvious that the problem is too much friction in the pivots.

The trick is to use the spring to support the weight of the balance. I am testing it by completely disengaging the escape wheel and measuring how many ticks the balance will swing for on its own. It was 11 at first, but by tweaking the spring so that it takes more of the weight I have got it up to 20. This drops to 5 if I add weight to the balance.

I think I also want a stronger spring than this one. Maybe I just take a few coils out of this one? By cutting it shorter and then straightening a new bit out. That way it would give the balance more dominion, and it would take more weight.

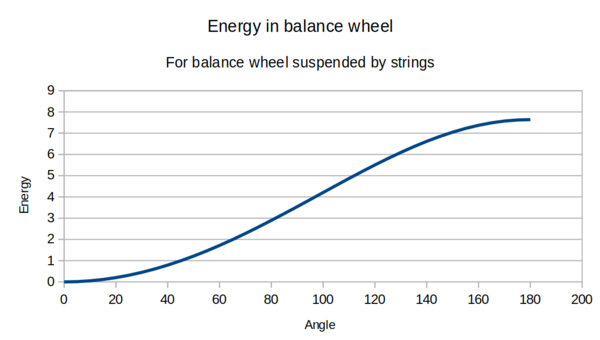
Before I do that: if you have a balance wheel suspended by 2 strings (like in 2024-06-18) but you don't allow them to get twisted (i.e. keep amplitude below 360 deg.), what kind of spring does that act like?

As the balance wheel rotates the strings lift it up slightly, so its weight is acting like a spring pulling it back towards the centre. But that might be good enough to use as the actual balance spring.

I remember doing some calculations with this before with ChatGPT, but can't find them in the notes, and wasn't confident I got it right.

Let's say all the string mounts are centered around the rotation axis, and symmetrical, and the 2 strings have equal length l. They are separated on the frame by d1 and on the balance wheel by d2. And the balance wheel angle is theta.

The balance wheel is at height h(theta) below the frame.

h(0) = sqrt(ll - (d2-d1)(d2-d1))

And the energy stored by the rising of the balance wheel is proportional to h(theta) - h(0), which is also proportional to the restoring torque (I think?).

So what is h(theta)?

In the h(0) formula, (d2-d1) is the distance between the top and bottom attachment points when viewed from above and projected on to the same plane. So we just need that but for some angle theta of the bottom point.

The top point is at (d1, 0) and the bottom point is at (d2 cos(theta), d2 sin(theta)).

So dx = (d2 cos(theta) - d1) and dy = d2 sin(theta)

I'll just make a spreadsheet to calculate the curve.

For a normal spring the curve would be a straight line, because the energy would be proportional to the spring extension.

But maybe this would work! I don't have a convenient way to test it now, so taking some coils out of the existing spring is a better thing to try.

Also I want to CAD up the stuff for the light gate quadrature thing, because it would be really useful to have it while testing these things. You could imagine a web UI that lets you select a time period and look at stats in it, like tick rate, tick rate standard deviation, amplitude, amplitude trend, etc, or show them for a live view with a sliding window or something.

The key thing I want to know at the moment is by what percentage the amplitude drops each cycle, for reducing the friction in the pivots.

I've now got it doing 45 or so ticks before stopping, this is a big improvement.

A couple of quick improvements:

• better shaft collars for the escape wheel: no screws because spring-load is enough, and no rubbing on the bearing
• a winding drum so that the torque is more consistent

And then a video clip, and then CAD the encoder holder thing.

It's working!! The winding drum made a world of difference. The string is no longer dragging against itself, and the increased radius means you get more torque for less weight, so less load on the bearings and frame for a given amount of torque, and it is ticking now at maybe 260 deg. amplitude? Great success.

https://www.youtube.com/watch?v=kejq3tOdtqs

I'm stopping for tonight. Can CAD the encoder holder tomorrow.

The video has 211 beats in 3m41s, which works out to about 1.05 seconds per beat.